题目内容
1.一个球的内接正方体的表面积为54,则球的表面积为 ( )| A. | 27π | B. | 18π | C. | 9π | D. | 54π |
分析 先设正方体的边长为a,根据正方体的表面积S=6a2=54,求得a=3,再根据正方体的体对角线长等于其外接球的直径,求得外接球的半径R,代入球的表面积公式计算.
解答 解:设正方体的边长为a,则正方体的表面积S=6a2=54,
∴a=3,又正方体的体对角线长等于其外接球的直径,
∴外接球的半径R=$\frac{3\sqrt{3}}{2}$,
∴其外接球的表面积为4π×$(\frac{3\sqrt{3}}{2})^{2}$=27π.
故选A.
点评 本题考查了正方体的表面积,正方体的外接球的表面积,解题的关键是利用正方体的体对角线长等于其外接球的直径,求得外接球的半径.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.已知直线l与坐标轴不垂直且横、纵截距相等,圆C:(x+1)2+(y-2)2=r2,若直线l和圆C相切,且满足条件的直线l恰好有三条,则圆的半径r的取值集合为( )
| A. | $\left\{{1,\sqrt{5}}\right\}$ | B. | $\left\{{\sqrt{5},\frac{{\sqrt{2}}}{2}}\right\}$ | C. | $\left\{{1,\sqrt{5},\frac{{\sqrt{2}}}{2}}\right\}$ | D. | $\left\{{1,2,\sqrt{5},\frac{{\sqrt{2}}}{2}}\right\}$ |
16.下列以x为自变量的函数中,是指数函数的是( )
| A. | $\begin{array}{l}\\ y={3^x}\end{array}$ | B. | y=(-3)x | C. | y=2x+1 | D. | y=x3 |
13.已知平面α内有一点M(1,-1,2),平面α的一个法向量$\overrightarrow n$=(2,-1,2),则下列点P在平面α内的是( )
| A. | (-4,4,0) | B. | (2,0,1) | C. | (2,3,3) | D. | (3,-3,4) |
10.从装有2个红球和 2个白球的口袋内任取2个,则互斥但不对立的两个事件是( )
| A. | 至少一个白球与都是白球 | B. | 至少一个白球与至少一个红球 | ||
| C. | 恰有一个白球与 恰有2个白球 | D. | 至少一个白球与都是红球 |
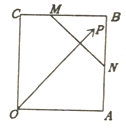 如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$.
如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$.