题目内容
20.已知集合A={x|log2x>0},B={x|x<1},则( )| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
分析 直接解对数不等式化简集合A,又已知集合B={x|x<1},则答案可求.
解答 解:A={x|log2x>0}={x|x>1},B={x|x≤1},
则A∩B=∅,A∪B={x|x>1或x<1}≠R.
故选:A.
点评 本题考查了交集、并集及其运算,熟练掌握交集及并集的定义是解本题的关键,是基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
11.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0)的图象与函数g(x)=cos(2x+φ)(|φ|<$\frac{π}{2}$)的图象的对称中心完全相同,则φ=( )
| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
8.已知复数z=$\frac{1}{i-1}$,则( )
| A. | z的实部为$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{\sqrt{2}}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
5.若复数z满足(1+2i)z=(1-i),则|z|=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\sqrt{10}$ |
10.从1,2,3,…,7共7个数字中任取3个不同的数字,则这3个数字由小到大可组成等差数列的概率为( )
| A. | $\frac{11}{35}$ | B. | $\frac{9}{35}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{7}$ |
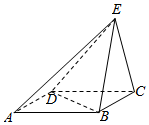 如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知$AB=2BC=4,BD=2\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.