题目内容
若实x,y数满足3x2+2y2≤6,则2x+y的最大值为 .
考点:基本不等式
专题:圆锥曲线中的最值与范围问题
分析:由实数x,y满足3x2+2y2≤6,可化为
+
≤1.可知:点P在椭圆
+
=1上或其内部.令2x+y=t,与椭圆的方程联立,令△≥0解出即可.
| y2 |
| 3 |
| x2 |
| 2 |
| y2 |
| 3 |
| x2 |
| 2 |
解答:
解:由实数x,y满足3x2+2y2≤6,化为
+
≤1.
可知:点P在椭圆
+
=1上或其内部.
令2x+y=t,
联立
,
化为11x2-8tx+2t2-6=0,
令△=64t2-44(2t2-6)≥0,
解得-
≤t≤
.
故当直线与椭圆相切取得最值时,其最大值为
.
故答案为:
.
| y2 |
| 3 |
| x2 |
| 2 |
可知:点P在椭圆
| y2 |
| 3 |
| x2 |
| 2 |
令2x+y=t,
联立
|
化为11x2-8tx+2t2-6=0,
令△=64t2-44(2t2-6)≥0,
解得-
| 11 |
| 11 |
故当直线与椭圆相切取得最值时,其最大值为
| 11 |
故答案为:
| 11 |
点评:本题考查了直线与椭圆的位置关系转化为方程联立得到△≥0及其转化能力,属于中档题.

练习册系列答案
相关题目
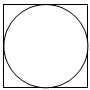 一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
一次实验:向如图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为N粒,其中m(m<N)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为
从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在复平面内,复数i(2+3i)对应点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |