题目内容
在△ABC中，内角A，B，C的对边分别是a，b，c，若2sinA=sinC，a2，c2，b2成等差数列，则B=（ ）
| A、30° | B、60° |
| C、120° | D、150° |
考点：正弦定理,余弦定理
专题：解三角形
分析：先利用正弦定理和已知等式求得a和c的关系，进而根据a2，c2，b2成等差数列，求得b和a的关系，最后代入余弦定理中求得cosB的值，则B可求．
解答：
解：∵2sinA=sinC，
∴2a=c，
∵2c2=a2+b2，
∴b2=4c2-a2=3a2
∴cosB=
=
=
，
∴B=
故选B．
∴2a=c，
∵2c2=a2+b2，
∴b2=4c2-a2=3a2
∴cosB=
| a2+c2-b2 |
| 2ac |
| a2+4a2-3a2 |
| 4a2 |
| 1 |
| 2 |
∴B=
| π |
| 3 |
故选B．
点评：本题主要考查了正弦定理和余弦定理的应用．正弦定理和余弦定理时解三角形问题中进行边角问题互化的常用工具．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
若a4（x+1）4+a3（x+1）3+a2（x+1）2+a1（x+1）+a0=x4，则a3+a2+a1的值为（ ）
| A、-2 | B、-1 | C、0 | D、1 |
已知等比数列{an}中，其前n项和Sn=3n+k，则k的值为（ ）
| A、-1 | B、1 | C、0 | D、3 |
等差数列{an}，前n项和为Sn，a1＞0，a2012，a2013是方程x2-（λ2+λ+1）x-（λ2+1）=0的两根，则满足Sn＞0的n的最大正整数为（ ）
| A、4023 | B、4024 |
| C、4025 | D、4026 |
我们知道十进制数有10个数码即0～9，进位规则是“逢十进一”，如47+56=103；由此可知八进制数有8个数码即0～7，进位规则是“逢八进一”，则在八进制下做如下运算47+56=（ ）
| A、85 | B、103 |
| C、125 | D、185 |
在△ABC中，sinC=2sinAcosB，则△ABC的形状为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、不能确定 |
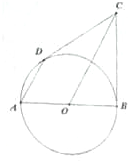如图，AB为圆O的直径，BC与圆O相切于点B，D为圆O上的一点，AD∥OC，连接CD．