题目内容
已知函数f(x)=log
[
sin(x-
)].
(1)求它的定义域和值域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的最小正周期.
| 1 |
| 2 |
| 2 |
| π |
| 4 |
(1)求它的定义域和值域;
(2)求它的单调区间;
(3)判断它的奇偶性;
(4)判断它的周期性,如果是周期函数,求出它的最小正周期.
考点:对数函数图象与性质的综合应用,复合三角函数的单调性
专题:函数的性质及应用
分析:(1)根据函数成立的条件即可求它的定义域和值域;
(2)利用复合函数单调性之间的关系,即可求它的单调区间;
(3)根据函数奇偶性的定义和性质即可判断它的奇偶性;
(4)根据函数周期性的定义即可判断它的周期性.
(2)利用复合函数单调性之间的关系,即可求它的单调区间;
(3)根据函数奇偶性的定义和性质即可判断它的奇偶性;
(4)根据函数周期性的定义即可判断它的周期性.
解答:
解:(1)要使函数有意义,则
sin(x-
)>0,
即sin(x-
)>0,
即2kπ<x-
<2kπ+π,k∈Z,
即2kπ+
<x<2kπ+
,k∈Z
∴函数的定义域为(2kπ+
,2kπ+
)(k∈Z).
∵0<
sin(x-
)≤
,
∴f(x)=log
[
sin(x-
)]≥log
=-
,
即函数f(x)的值域是[-
,+∞).
(2)∵当2kπ+
<x<2kπ+
时,函数t=
sin(x-
)为增函数,而y=log
t为减函数,
∴根据复合函数的单调性可知,此时函数f(x)=log
[
sin(x-
)]单调递减.
∵当2kπ+
<x<2kπ+
时,函数t=
sin(x-
)为减函数,而y=log
t为减函数,
∴根据复合函数的单调性可知,此时函数f(x)=log
[
sin(x-
)]单调递增.
∴单调递增区间是(2kπ+
,2kπ+
)(k∈Z),
单调递减区间是(2kπ+
,2kπ+
)(k∈Z).
(3)因为f(x)定义域在数轴上对应的点不关于原点对称,
故f(x)是非奇非偶函数.
(4)∵f(x+2π)=log
[
sin(x+2π-
)]=log
[
sin(x-
)]=f(x),
∴函数f(x)的最小正周期T=2π.
| 2 |
| π |
| 4 |
即sin(x-
| π |
| 4 |
即2kπ<x-
| π |
| 4 |
即2kπ+
| π |
| 4 |
| 5π |
| 4 |
∴函数的定义域为(2kπ+
| π |
| 4 |
| 5π |
| 4 |
∵0<
| 2 |
| π |
| 4 |
| 2 |
∴f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
即函数f(x)的值域是[-
| 1 |
| 2 |
(2)∵当2kπ+
| π |
| 4 |
| 3π |
| 4 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴根据复合函数的单调性可知,此时函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
∵当2kπ+
| 3π |
| 4 |
| 5π |
| 4 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴根据复合函数的单调性可知,此时函数f(x)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
∴单调递增区间是(2kπ+
| 3π |
| 4 |
| 5π |
| 4 |
单调递减区间是(2kπ+
| π |
| 4 |
| 3π |
| 4 |
(3)因为f(x)定义域在数轴上对应的点不关于原点对称,
故f(x)是非奇非偶函数.
(4)∵f(x+2π)=log
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2 |
| π |
| 4 |
∴函数f(x)的最小正周期T=2π.
点评:本题主要考查函数的性质的综合判断,要求熟练掌握函数单调性,奇偶性,周期性以及定义域,值域的求解和判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,AB∥CD且∠ADC=90°,AD=1,CD=
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,AB∥CD且∠ADC=90°,AD=1,CD=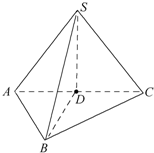 已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.
已知直角△ABC所在平面外一点S,且SA=SB=SC,D为斜边AC中点.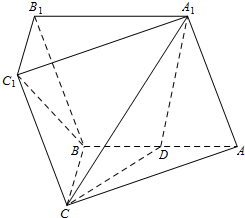 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,且∠A1AB=60°,AC=BC,D是AB的中点. 如图所示,P是△ABC内一点,且满足
如图所示,P是△ABC内一点,且满足