题目内容
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
B
解析试题分析:由题意可知
 =(2,1),(2,3),(4,1),(4,3),从中取两个向量,基本事件总数为6,分别为(2,1)和(2,3);(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,1);(2,3)和(4,3);(4,1)和(4,3),其中,当所取的向量为(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,3)时,所得三角形
=(2,1),(2,3),(4,1),(4,3),从中取两个向量,基本事件总数为6,分别为(2,1)和(2,3);(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,1);(2,3)和(4,3);(4,1)和(4,3),其中,当所取的向量为(2,1)和(4,1);(2,1)和(4,3);(2,3)和(4,3)时,所得三角形 面积为1,所以
面积为1,所以
 ,选B,如图所示
,选B,如图所示
在图1中, ,在图2中,
,在图2中, ,选B.
,选B.
考点:1、向量;2、图形的面积;3、古典概型.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设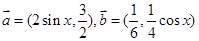 ,且
,且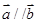 ,则锐角
,则锐角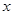 为( )
为( )
A.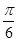 | B.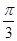 | C.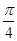 | D.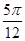 |
若两个非零向量 ,
, 满足
满足 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
如图,在 中,点
中,点 是
是 边上靠近
边上靠近 的三等分点,则
的三等分点,则 ( )
( )
A. | B. | C. | D. |
设O是正△ABC的中心,则向量 ,
, ,
, 是( )
是( )
| A.相等向量 | B.模相等的向量 |
| C.共线向量 | D.共起点的向量 |
在 中,
中,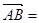 c,
c, b。若点D满足
b。若点D满足
A. b+ b+ c c | B. c c b b | C. b b c c | D. b b c c |
如图,网格纸上小正方形的边长为 ,粗线画出的是某几何体的
,粗线画出的是某几何体的
三视图,则此几何体的体积为( )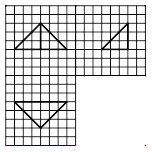
A. | B. | C. | D. |
等边△ABC的边长为2,平面内一点 满足
满足 =( )
=( )
A. | B.— | C. | D.— |
 =a1
=a1 +a4021
+a4021 ,其中{an}为等差数列,则a2011等于( )
,其中{an}为等差数列,则a2011等于( )