题目内容
若两个非零向量 ,
, 满足
满足 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
B
解析试题分析:两个非零向量 ,
, 满足
满足 ,由向量的加法与减法的几何意义可知,
,由向量的加法与减法的几何意义可知,

 ,又因为
,又因为 ,所以
,所以 与
与 的夹角为
的夹角为 .
.
考点:向量的加法与减法的几何意义.

练习册系列答案
相关题目
设向量 =(sinα,
=(sinα, )的模为
)的模为 ,则cos2α=( )
,则cos2α=( )
A. | B. | C.﹣ | D.﹣ |
已知向量 满足
满足 ,且
,且 ,则
,则 在
在 方向上的投影为( )
方向上的投影为( )
| A.3 | B. . . | C. | D. |
已知 为等边三角形,
为等边三角形,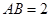 ,设
,设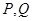 满足
满足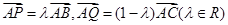 ,若
,若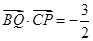 ,则
,则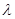 等于( )
等于( )
A.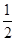 | B.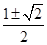 | C.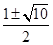 | D.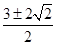 |
如图,已知点 是边长为1的等边
是边长为1的等边 的中心,则
的中心,则 等于( )
等于( )
A. | B. | C. | D. |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
已知 ,若
,若 =
= ,
,
 ,则
,则 =( )(用
=( )(用 ,
, 表示)
表示)
A.- | B. |
C. | D. |
已知点A(1,3),B(4,-1),则与向量 同方向的单位向量为( )
同方向的单位向量为( )
A. | B. |
C. | D. |
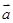 -
-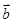 等于 ( )
等于 ( ) 



