题目内容
如图,网格纸上小正方形的边长为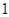 ,粗线画出的是某几何体的
,粗线画出的是某几何体的
三视图,则此几何体的体积为( )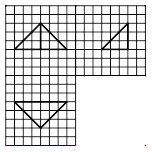
A.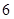 | B.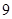 | C. | D.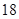 |
B
解析试题分析:该几何体为三棱锥,底面等腰三角形底边长为6,高为3;一条侧棱垂直于底面,几何体的高3,所以,几何体的体积为 =9,故选B。
=9,故选B。
考点:三视图,几何体的体积。
点评:简单题,三视图问题已成为高考必考知识内容,一般难度不大。关键是明确三视图画法规则,掌握常见几何体的几何特征。三视图中的虚线是被遮住的棱。

练习册系列答案
相关题目
设向量 =(sinα,
=(sinα, )的模为
)的模为 ,则cos2α=( )
,则cos2α=( )
A. | B. | C.﹣ | D.﹣ |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
已知 ,若
,若 =
= ,
,
 ,则
,则 =( )(用
=( )(用 ,
, 表示)
表示)
A.- | B. |
C. | D. |
化简下列式子:其结果为零向量的个数是( )
① ; ②
; ② ;
;
③ ; ④
; ④
| A.1 | B.2 | C.3 | D.4 |
若平行四边形的3个顶点分别是(4,2),(5,7),( 3,4),则第4个顶点的坐标不可能是( )
3,4),则第4个顶点的坐标不可能是( )
| A.(12,5) | B.(-2,9) | C.(3,7) | D.(-4,-1) |
设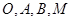 为平面上四点,
为平面上四点,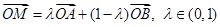 ,则
,则
A.点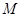 在线段 在线段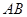 上 上 | B.点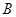 在线段 在线段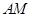 上 上 |
C.点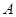 在线段 在线段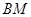 上 上 | D.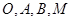 四点共线 四点共线 |
如图,在 中,
中, ,延长CB到D,使
,延长CB到D,使 ,则
,则 的值是 ( )
的值是 ( )
| A.1 | B.3 | C.-1 | D.2 |
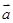 -
-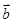 等于 ( )
等于 ( ) 



