题目内容
在 中,
中,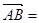 c,
c, b。若点D满足
b。若点D满足
A. b+ b+ c c | B. c c b b | C. b b c c | D. b b c c |
A
解析试题分析:把向量用一组向量来表示,做法是从要求向量的起点出发,尽量沿着已知向量,走到要求向量的终点,把整个过程写下来,即为所求.本题也可以根据D点把BC分成一比二的两部分入手.因为 ,故选A.
,故选A.
考点:向量的加减运算
点评:用一组向量来表示一个向量,是以后解题过程中常见到的,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的

练习册系列答案
相关题目
在平面直角坐标系中,已知向量 若
若 ,则x=( )
,则x=( )
| A.-2 | B.-4 | C.-3 | D.-1 |
已知 为等边三角形,
为等边三角形,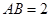 ,设
,设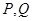 满足
满足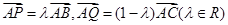 ,若
,若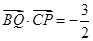 ,则
,则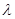 等于( )
等于( )
A.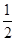 | B.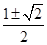 | C.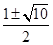 | D.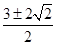 |
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
已知直线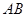 与抛物线
与抛物线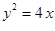 交于
交于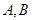 两点,
两点,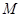 为
为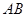 的中点,
的中点,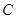 为抛物线上一个动点,若
为抛物线上一个动点,若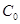 满足
满足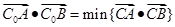 ,则下列一定成立的是( )。
,则下列一定成立的是( )。
A.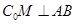 | B.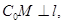 其中 其中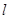 是抛物线过 是抛物线过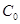 的切线 的切线 |
C.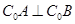 | D.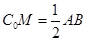 |
已知 ,若
,若 =
= ,
,
 ,则
,则 =( )(用
=( )(用 ,
, 表示)
表示)
A.- | B. |
C. | D. |
化简下列式子:其结果为零向量的个数是( )
① ; ②
; ② ;
;
③ ; ④
; ④
| A.1 | B.2 | C.3 | D.4 |
设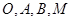 为平面上四点,
为平面上四点,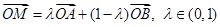 ,则
,则
A.点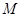 在线段 在线段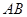 上 上 | B.点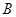 在线段 在线段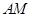 上 上 |
C.点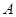 在线段 在线段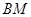 上 上 | D.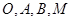 四点共线 四点共线 |
在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |