题目内容
等边△ABC的边长为2,平面内一点 满足
满足 =( )
=( )
A. | B.— | C. | D.— |
D
解析试题分析:利用向量的运算法则将 分别用等边三角形的边对应的向量表示,利用向量的运算法则展开,据三角形的边长及边边的夹角已知,求出两个向量的数量积.
分别用等边三角形的边对应的向量表示,利用向量的运算法则展开,据三角形的边长及边边的夹角已知,求出两个向量的数量积.
因为
 夹角为60度,长度都是2,则利用数量积公式得到
夹角为60度,长度都是2,则利用数量积公式得到 ,代入上式可知结论为—
,代入上式可知结论为— ,选D.
,选D.
考点:本试题主要考查了向量的数量积的基本运算.考查了基本知识的综合运用能力.
点评:解决该试题的关键将所求的向量运用平面向量的基本定理表示为一组基底来得到。

练习册系列答案
相关题目
在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量α=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作三角形,事件“所得三角形的面积等于1”的概率为 ( )
A. | B. | C. | D. |
设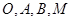 为平面上四点,
为平面上四点,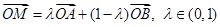 ,则
,则
A.点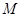 在线段 在线段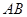 上 上 | B.点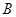 在线段 在线段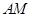 上 上 |
C.点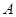 在线段 在线段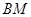 上 上 | D.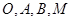 四点共线 四点共线 |
若 为
为 所在平面内一点,且满足
所在平面内一点,且满足 ,
, ,则
,则 ABC的形状为
ABC的形状为
| A.正三角形 | B.直角三角形 | C.等腰三角形 | D.等腰直角三角形 |
 中,
中, 边的高为
边的高为 ,若
,若 ,
, ,
, ,
, ,
, ,则
,则 ( )
( )
A. | B. |
C. | D. |
在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |
如图,在 中,
中, ,延长CB到D,使
,延长CB到D,使 ,则
,则 的值是 ( )
的值是 ( )
| A.1 | B.3 | C.-1 | D.2 |
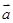 -
-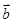 等于 ( )
等于 ( ) 




 同向的单位向量是
同向的单位向量是 ,
, _
_ ) B(-
) B(- ) C(-
) C(- ) D(
) D( )
)