已知$m=a+\frac{1}{a-2}$.$n={2^{2-{b^2}}}$.m的最小值为:4.则m.n之间的大小关系为m＞n．题目和参考答案——青夏教育精英家教网——

题目内容

16．已知$m=a+\frac{1}{a-2}（a＞2）$，$n={2^{2-{b^2}}}（b≠0）$，m的最小值为：4，则m，n之间的大小关系为m＞n．

分析利用基本不等式的性质、指数函数的单调性即可得出．

解答解：∵$m=a+\frac{1}{a-2}（a＞2）$，
∴m=a-2+$\frac{1}{a-2}$+2≥2$\sqrt{（a-2）•\frac{1}{a-2}}$+2=4，当且仅当a=4时取等号．
∵$n={2^{2-{b^2}}}（b≠0）$，∴n＜2²=4．
故答案为：4，m＞n．

点评本题考查了基本不等式的性质、指数函数的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案

尖子生超级训练系列答案

减负增效拓展三阶训练系列答案

江苏13大市中考28套卷系列答案

天利38套中考试题精粹系列答案

教材解读与拓展系列答案

教材快线系列答案

教材完全学案系列答案

精析巧练系列答案

今日课堂课时作业系列答案

金版卷王课程探究大试卷系列答案

相关题目

6．已知数列{a_n}的通项公式是a_n=$\left\{\begin{array}{l}{2^{-n}}\;\;\;\;\;\;（n是奇数）\\ \frac{1}{{2n+{n^2}}}\;\;（n是偶数）\end{array}$，则它的前4项和为$\frac{19}{24}$．

7．已知向量$\overrightarrow a$=（$\sqrt{3}$sin3x，-y），$\overrightarrow b$=（m，cos3x-m）（m∈R），且$\overrightarrow a$+$\overrightarrow b$=$\overrightarrow 0$．设y=f（x）．
（1）求f（x）的表达式，并求函数f（x）在[${\frac{π}{18}$，$\frac{π}{3}}$]上图象最低点M的坐标．
（2）在△ABC中，f（A）=-$\sqrt{3}$，且A＞$\frac{4}{9}$π，D为边BC上一点，AC=$\sqrt{3}$DC，BD=2DC，且AD=2$\sqrt{2}$，求线段DC的长．

4．已知$tanα=\frac{1}{2}，sin（α+β）=-\frac{{\sqrt{2}}}{10}$，其中α，β∈（0，π）．
（1）求cosβ的值；
（2）求α-β的值．

11．已知向量$\overrightarrow a≠\overrightarrow e$，$|\overrightarrow e|=1$，对任意t∈R，恒有$|\overrightarrow a-t\overrightarrow e|≥|\overrightarrow a-2\overrightarrow e|$，则（　　）

$\overrightarrow a⊥\overrightarrow e$

$\overrightarrow a⊥（\overrightarrow a-2\overrightarrow e）$

$\overrightarrow e⊥（\overrightarrow a-2\overrightarrow e）$

$（\overrightarrow a+2\overrightarrow e）⊥（\overrightarrow a-2\overrightarrow e）$

1．若$x\;{（1-mx）^{\;4}}={a_1}\;x+{a_2}\;{x^2}+{a_3}\;{x^3}+{a_4}\;{x^4}+{a_5}\;{x^5}$，其中a₂=-6，则实数m=$\frac{3}{2}$；a₁+a₃+a₅=$\frac{313}{16}$．

8．已知集合A={log₂x，4，8}，B={4，5}．若A∪B={1，4，5，8}，则实数x的值为2，A∩B={4}；令U=A∪B，则∁_UA={5}．

5．已知函数f（x）=e^x+ax，（a∈R），其图象与x轴交于A（x₁，0），B（x₂，0）两点，且x₁＜x₂．
（1）证明：a＜-e；
（2）证明：$f'（{\frac{{{x_1}+{x_2}}}{2}}）＜0$；（其中f'（x）为f（x）的导函数）．
（3）设点C在函数f（x）的图象上，且△ABC为等边三角形，记$\sqrt{\frac{x_2}{x_1}}=t$，求$（t-1）（a+\sqrt{3}）$的值．

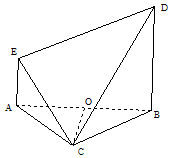如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，AE⊥AB，BC=BD=2AE=2，O为AB的中点．
（1）证明：CO⊥DE；
（2）求二面角C-DE-A的大小．