题目内容
设等比数列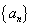 的首项为
的首项为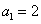 ,公比为
,公比为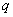 (
(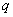 为正整数),且满足
为正整数),且满足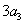 是
是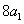 与
与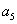 的
的 等差中项;等差数列
等差中项;等差数列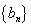 满足
满足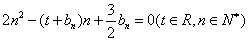 .
.
(1)求数列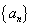 ,
,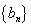 的通项公式;
的通项公式;
(2) 若对任意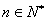 ,有
,有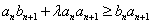 成立,求实数
成立,求实数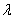 的取值范围;
的取值范围;
(3)对每个正整数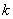 ,在
,在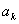 和
和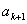 之间插入
之间插入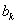 个2,得到一个新数列
个2,得到一个新数列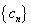 ,设
,设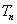 是数列
是数列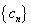 的前
的前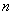 项和,试求满足
项和,试求满足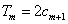 的所有正整数
的所有正整数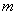 .
.
(1)由题意 ,则
,则 ,解得
,解得 或
或
因为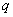 为正整数,所以
为正整数,所以 , 又
, 又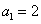 ,所以
,所以

(2) .
.
记 当
当 时
时 ,得
,得 单调减,
单调减,
又 ,所以
,所以
(3)由题意知,
则当 时,
时, ,不合题意,舍去;
,不合题意,舍去;
当 时,
时, ,所以
,所以 成立;
成立;
当 时,若
时,若 ,则
,则 ,不合题意,舍去;从而
,不合题意,舍去;从而 必是数列
必是数列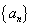 中的某一项
中的某一项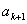 ,则
,则



又 ,所以
,所以
 ,
,
即 ,所以
,所以
因为 为奇数,而
为奇数,而 为偶数,所以上式无解。
为偶数,所以上式无解。
即当 时,
时,
综上所述,满足题意的正整数仅有 .
.

练习册系列答案
相关题目
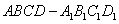 中,
中, 、
、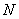 分别是
分别是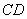 、
、 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小是________.
所成角的大小是________.
 ,椭圆
,椭圆 ,
, 分别为椭圆
分别为椭圆 的左、右焦点.
的左、右焦点.  过右焦点
过右焦点 时,求直线
时,求直线 交于
交于 两点,
两点, ,的重心分别为
,的重心分别为 .若原点
.若原点 在以线段
在以线段 为直径的圆内,求实数
为直径的圆内,求实数 的取值范围.
的取值范围. 
 是公差不为0的等差数列,
是公差不为0的等差数列, 是等比数列,其中
是等比数列,其中 ,
, ,
, ,
, ,且存在常数
,且存在常数 ,
, ,使得
,使得 对每一个正整数
对每一个正整数 =________.
=________. ,若
,若 .
. 与
与 ;
; ,记数列
,记数列 的前
的前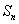
 )求
)求 )求正整数
)求正整数 ,均有
,均有 .
. ;②
;② ;③
;③ ;④
;④ ,则使函数y=lnt的值域为R的代换有_______.
,则使函数y=lnt的值域为R的代换有_______. )<0成立,则实数m的取值范围是________.
)<0成立,则实数m的取值范围是________. 的图像关于直线
的图像关于直线 对称,则
对称,则 .
.
 个单位长度后,所得的函数恰好是偶函数,则φ的值为________.
个单位长度后,所得的函数恰好是偶函数,则φ的值为________.