题目内容
如果对任意的x，y∈R都有f（x+y）=f（x）•f（y），且f（1）=2，
（1）求f（0），f（2），f（3）的值和
+
+
+…+
的值；
（2）若当x＞0时，有f（x）＞1成立，试判断函数f（x）在区间（0，+∞）上的单调性并加以证明．
（1）求f（0），f（2），f（3）的值和
| f(2) |
| f(1) |
| f(3) |
| f(2) |
| f(4) |
| f(3) |
| f(2013) |
| f(2012) |
（2）若当x＞0时，有f（x）＞1成立，试判断函数f（x）在区间（0，+∞）上的单调性并加以证明．
考点：抽象函数及其应用
专题：计算题,函数的性质及应用
分析：（1）令x=1，y=0，求出f（0），令x=y=1，求出f（2），令x=1，y=2求出f（3）；由
=f（1）=2，即可求出所求的和；
（2）运用单调性定义证明，令x1＞x2＞0，则x1-x2＞0，?x＞0，f（x）=f2（
）≥0，证明不能为0，再由f（x1）=
f（x1-x2）f（x2）＞f（x2），即可得到单调性．
| f(n+1) |
| f(n) |
（2）运用单调性定义证明，令x1＞x2＞0，则x1-x2＞0，?x＞0，f（x）=f2（
| x |
| 2 |
f（x1-x2）f（x2）＞f（x2），即可得到单调性．
解答：
解：（1）令x=1，y=0，则f（1）=f（1）f（0），
由于f（1）=2，则f（0）=1，
又∵对任意的x，y∈R都有f（x+y）=f（x）•f（y），且f（1）=2，
∴f（2）=f（1）f（1）=4，f（3）=f（1）f（2）=8，
∴
=2，
=f（1）=2，
∴
+
+
+…+
=2012f（1）=4024；
（2）函数f（x）在区间（0，+∞）上是增函数．
理由：令x1＞x2＞0，则x1-x2＞0，而f（x+y）=f（x）•f（y），
∴f（x1）=f（x1-x2+x2）=f（x1-x2）f（x2）
∵?x＞0，f（x）=f2（
）≥0，若存在x0，使f（x0）=0，
则f（1）=f（x0）f（1-x0）=0这与f（1）=2矛盾，
∴f（x）＞0恒成立，
由x＞0，f（x）＞1，∴f（x1-x2）＞1，f（x2）＞0，
∴f（x1）=f（x1-x2）f（x2）＞f（x2），
∴函数f（x）在区间（0，+∞）上是增函数．
由于f（1）=2，则f（0）=1，
又∵对任意的x，y∈R都有f（x+y）=f（x）•f（y），且f（1）=2，
∴f（2）=f（1）f（1）=4，f（3）=f（1）f（2）=8，
∴
| f(2) |
| f(1) |
| f(n+1) |
| f(n) |
∴
| f(2) |
| f(1) |
| f(3) |
| f(2) |
| f(4) |
| f(3) |
| f(2013) |
| f(2012) |
（2）函数f（x）在区间（0，+∞）上是增函数．
理由：令x1＞x2＞0，则x1-x2＞0，而f（x+y）=f（x）•f（y），
∴f（x1）=f（x1-x2+x2）=f（x1-x2）f（x2）
∵?x＞0，f（x）=f2（
| x |
| 2 |
则f（1）=f（x0）f（1-x0）=0这与f（1）=2矛盾，
∴f（x）＞0恒成立，
由x＞0，f（x）＞1，∴f（x1-x2）＞1，f（x2）＞0，
∴f（x1）=f（x1-x2）f（x2）＞f（x2），
∴函数f（x）在区间（0，+∞）上是增函数．
点评：本题考查抽象函数及应用，考查解决抽象函数的常用方法：赋值法，同时考查函数的单调性及证明，注意定义的运用，属于中档题．
练习册系列答案
相关题目
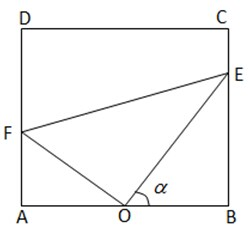南海中学校园内建有一块矩形草坪ABCD，AB=50米，BC=25