题目内容
已知函数f(x)=x+
+alnx
(1)若f(x)在x=1处取得极值.求a的值;
(2)若f(x)在[1,2]上为减函数,求a的取值范围;
(3)若g(x)=f(x)-x,当a>0时,是否存在a使得g(x)在(0,e]上有最小值0,若存在,求出a的值;若不存在,说明理由.
| 2 |
| x |
(1)若f(x)在x=1处取得极值.求a的值;
(2)若f(x)在[1,2]上为减函数,求a的取值范围;
(3)若g(x)=f(x)-x,当a>0时,是否存在a使得g(x)在(0,e]上有最小值0,若存在,求出a的值;若不存在,说明理由.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)求导函数,利用f(x)在x=1处取得极值.建立方程,可求a、b的值
(2)若f(x)在[1,2]上为减函数,则f′(x)=1-
+
≤0恒成立,利用分离参数法得出a≤
-x,只需a≤(
-x)min,转化为求≤(
-x)min
(3)g(x)=f(x)-x=
+alnx,g′(x)=-
+
=
.由ax-2=0,得x=
.分0<
<e,
≥e分别求出最小值,解关于a的方程得出a
(2)若f(x)在[1,2]上为减函数,则f′(x)=1-
| 2 |
| x2 |
| a |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
(3)g(x)=f(x)-x=
| 2 |
| x |
| 2 |
| x2 |
| a |
| x |
| ax-2 |
| x2 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
解答:
解:(1)求导函数,f′(x)=1-
+
,f(x)在x=1处取得极值,f′(1)=0,a=1.
(2)若f(x)在[1,2]上为减函数,则f′(x)=1-
+
≤0恒成立,即x2+ax-2≤0,
a≤
-x,只需a≤(
-x)min,(
-x)′=-
-1<0,
-x单调递减,当x=2时,(
-x)min,=-1,
所以a的取值范围a≤-1;
(3)g(x)=f(x)-x=
+alnx,g′(x)=-
+
=
.
由ax-2=0,得x=
(>0),
当0<
<e①时,若x∈(0,
)则g′(x)<0,若x∈(
,e)则g′(x)>0,
所以此时g(x)最小值=g(
)=a+aln
=0,
=
,a=2e,符合①.
当
≥e②时,g′(x)<0,此时g(x)最小值=g(e)=
+a=0,a=-
(舍去)
综上所述,a=2e.
| 2 |
| x2 |
| a |
| x |
(2)若f(x)在[1,2]上为减函数,则f′(x)=1-
| 2 |
| x2 |
| a |
| x |
a≤
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x2 |
| 2 |
| x |
| 2 |
| x |
所以a的取值范围a≤-1;
(3)g(x)=f(x)-x=
| 2 |
| x |
| 2 |
| x2 |
| a |
| x |
| ax-2 |
| x2 |
由ax-2=0,得x=
| 2 |
| a |
当0<
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
所以此时g(x)最小值=g(
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 1 |
| e |
当
| 2 |
| a |
| 2 |
| e |
| 2 |
| e |
综上所述,a=2e.
点评:本题考查导数知识的综合运用,考查函数的极值求解,不等式恒成立,分类讨论的能力.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
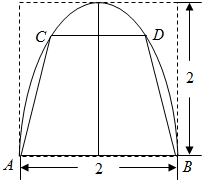 如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的轴对称,且AB=2,抛物线的顶点到底边的距离是2,记CD=2t,梯形面积为S.
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的轴对称,且AB=2,抛物线的顶点到底边的距离是2,记CD=2t,梯形面积为S.