题目内容
13.已知椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两焦点分别为F1,F2,其离心率为$\frac{\sqrt{3}}{2}$,椭圆G上一点M满足$\overrightarrow{{MF}_{1}}•\overrightarrow{{MF}_{2}}$=0.且△MF1F2的面积为1.(I)求椭圆G的方程;
(Ⅱ)过椭圆G长轴上的点P(t,0)的直线l与圆O:x2+y2=1相切于点Q(P与Q不重合),交椭圆G于A,B两点,若|AQ|=|BP|,求实数t的值.
分析 (1)由椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,知a2=4b2,由$\overrightarrow{{MF}_{1}}•\overrightarrow{{MF}_{2}}$=0,知MF1⊥MF2,且△MF1F2的面积为1,知|MF1||MF2|=2.由此能导出椭圆G的方程;
(2)由题意设出l:y=k(x-t),得到OQ所在直线方程,求出Q的坐标,由直线和圆相切得到${k}^{2}=\frac{1}{{t}^{2}-1}$,再联立直线方程和椭圆方程,由|AQ|=|BP|可得AB中点与PQ中点重合,由此列式求得k值,代入${k}^{2}=\frac{1}{{t}^{2}-1}$求得t值.
解答 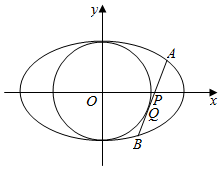 解:(Ⅰ))∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}$,即a2=4b2,①
解:(Ⅰ))∵$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}$,即a2=4b2,①
∵$\overrightarrow{{MF}_{1}}•\overrightarrow{{MF}_{2}}$=0,∴MF1⊥MF2,且△MF1F2的面积为1,
则${S}_{△M{F}_{1}{F}_{2}}$=$\frac{1}{2}$|MF1||MF2|=1,即|MF1||MF2|=2.
∵|MF1|+|MF2|=2a,
∴|MF1|2+2|MF1||MF2|+|MF2|2=4a2.
∴|F1F2|2+4=4a2.
∴4(a2-b2)+4=4a2,∴b2=1.②
将②代入①,得a2=4.
∴椭圆G的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)如图,由题意可知,直线l的斜率存在且不为0,设为k,
则l:y=k(x-t),
则OQ所在直线方程为y=-$\frac{1}{k}x$,
由O到直线l的距离d=$\frac{|-kt|}{\sqrt{{k}^{2}+1}}=1$,得${k}^{2}=\frac{1}{{t}^{2}-1}$,
联立$\left\{\begin{array}{l}{y=k(x-t)}\\{y=-\frac{1}{k}x}\end{array}\right.$,解得:Q($\frac{{k}^{2}t}{1+{k}^{2}},-\frac{kt}{1+{k}^{2}}$),
联立$\left\{\begin{array}{l}{y=k(x-t)}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2-8k2tx+4k2t2-4=0,
∴${x}_{1}+{x}_{2}=\frac{8{k}^{2}t}{1+4{k}^{2}}$,
由题意可知,AB中点与PQ中点重合,
则$\frac{4{k}^{2}t}{1+4{k}^{2}}=\frac{\frac{{k}^{2}t}{1+{k}^{2}}+t}{2}$,即${k}^{2}=\frac{1}{2}$.
代入${k}^{2}=\frac{1}{{t}^{2}-1}$,得t=$±\sqrt{3}$.
∴实数t的值为$±\sqrt{3}$.
点评 本题主要考查椭圆方程求法,考查直线与圆锥曲线的位置关系等知识,考查化归与转化、数形结合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力,是中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案| A. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | B. | $\frac{x^2}{25}+\frac{y^2}{16}$=1 | C. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{25}$=1 |
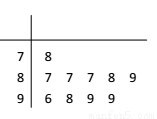
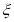 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求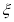 的分布列及数学期望.
的分布列及数学期望.