题目内容
5.在△ABC中,$\overrightarrow{AB}$$•\overrightarrow{AC}$=|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=2.(1)求|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2的值;
(2)若A=$\frac{π}{3}$,求△ABC三边的长.
分析 (1)对条件式两边平方即可解出;
(2)根据向量的数量积得出AB•AC,联立方程组解出AB,AC,BC=|$\overrightarrow{AB}-\overrightarrow{AC}$|=2.
解答 解:(1)∵$\overrightarrow{AB}$$•\overrightarrow{AC}$=|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=2,
∴|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2-2$\overrightarrow{AB}•\overrightarrow{AC}$=4,即|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2-4=4,
∴|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2=8.
(2)∵$\overrightarrow{AB}•\overrightarrow{AC}$=AB•AC•cosA=$\frac{1}{2}$AB•AC=2.
∴AB•AC=4.
∴(AB-AC)2=AB2+AC2-2AB•AC=0.
∴AB=AC=2.
BC=|$\overrightarrow{AB}-\overrightarrow{AC}$|=2.
点评 本题考查了平面向量的数量积运算,向量的三角形法则,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
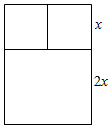 一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求:
一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求: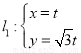 (
( 为参数),圆
为参数),圆 ,以坐标原点为极点,
,以坐标原点为极点, 轴的正半轴为极轴建立直角坐标系.
轴的正半轴为极轴建立直角坐标系.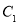 的极坐标方程,直线
的极坐标方程,直线 的极坐标方程;
的极坐标方程;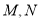 ,求
,求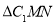 的面积.
的面积. ,求
,求 ( )
( )