题目内容
18.化简求值:(不用计算器)(1)$\frac{1+tan15°}{1-tan15°}$;
(2)$\frac{\sqrt{3}-tan15°}{1+\sqrt{3}tan15°}$;
(3)tan21°+tan24°+tan21°tan24°;
(4)tanα+tan($\frac{π}{3}$-α)+$\sqrt{3}$tanαtan($\frac{π}{3}$-α).
分析 (1)将题中特殊角的三角函数值代入原式,利用两角和的正切函数公式化简可得答案.
(2)将题中特殊角的三角函数值代入原式,利用两角差的正切函数公式化简可得答案.
(3)将题中特殊角的三角函数值代入原式,利用两角和的正切函数公式化简可得答案.
(4)利用两角和的正切函数公式化简可得答案.
解答 解:(1)$\frac{1+tan15°}{1-tan15°}$=$\frac{tan45°+tan15°}{1-tan45°tan15°}$=tan60°=$\sqrt{3}$;
(2)$\frac{\sqrt{3}-tan15°}{1+\sqrt{3}tan15°}$=$\frac{tan60°-tan15°}{1+tan60°tan15°}$=tan(60°-15°)=tan45°=1;
(3)tan21°+tan24°+tan21°tan24°=tan(21°+24°)(1-tan21°tan24°)+tan21°tan24°=1-tan21°tan24°+tan21°tan24°=1;
(4)tanα+tan($\frac{π}{3}$-α)+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=tan(α+$\frac{π}{3}$-α)(1-tanαtan($\frac{π}{3}$-α))+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=$\sqrt{3}$-$\sqrt{3}$tanαtan($\frac{π}{3}$-α)+$\sqrt{3}$tanαtan($\frac{π}{3}$-α)=$\sqrt{3}$.
点评 本题主要考查了特殊角的三角函数值,两角和的正切函数公式在三角函数化简求值中的应用,熟记特殊角的三角函数是解题的关键,属于基础题.

 阅读快车系列答案
阅读快车系列答案 满足约束条件
满足约束条件 ,那么
,那么 的最大值是__________.
的最大值是__________.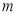 、
、 ,两个不同平面
,两个不同平面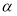 、
、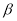 ,给出下列命题:
,给出下列命题: 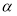 ;
;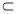
 ,
,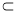
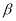 且
且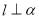 ,则
,则