题目内容
19．设等差数列{an}的前n项和Sn，若S1006＞S1008＞S1007，满足SnSn+1＜0的正整数n=2015．分析 由已知可得a1008＞0，a1007+a1008＜0，再由等差数列的性质和求和公式可得得S2015＞0，S2016＜0，可得结论．
解答 解：由题意可得S1008-S1007＞0，即a1008＞0，
再由若S1006＞S1008可得S1008-S1006＜0，即a1007+a1008＜0，
∴由等差数列的求和公式和性质可得S2015=$\frac{2015（{a}_{1}+{a}_{2015}）}{2}$=$\frac{2015×2{a}_{1008}}{2}$=2015a1008＞0，
同理可得S2016=$\frac{2016（{a}_{1}+{a}_{2016}）}{2}$=1008（a1007+a1008）＜0，
∴满足SnSn+1＜0的正整数n=2015，
故答案为：2015．
点评 本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
相关题目
13．若动点M（x，y）始终满足关系式$\sqrt{{x}^{2}+（y+2）^{2}}$+$\sqrt{{x}^{2}+（y-2）^{2}}$=8，则动点N的轨迹方程为（ ）
| A． | $\frac{x^2}{16}+\frac{y^2}{12}$=1 | B． | $\frac{x^2}{12}+\frac{y^2}{16}$=1 | C． | $\frac{x^2}{12}-\frac{y^2}{16}$=1 | D． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{12}$=1 |
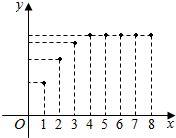甲工厂八年来某种产品年产量与时间（单位：年）的函数关系如图所示．现有下列四种说法：