题目内容
9.在△ABC中,a,b,c是角A、B、C的对边,且b=2asinB,A为锐角.(1)求角A的大小;
(2)若b=1,c=2$\sqrt{3}$,求a.
分析 (1)由已知利用正弦定理可得sinB=2sinA•sinB,结合sinB>0可得sinA=$\frac{1}{2}$,又A为锐角,即可解得A的值.
(2)利用余弦定理即可解得a的值.
解答 (本题满分为10分)
解:(1)在△ABC中,∵b=2asinB,
∴sinB=2sinA•sinB,sinB>0,
∴sinA=$\frac{1}{2}$,
∵A为锐角,
∴A=$\frac{π}{6}$…6分
(2)∵a2=b2+c2-2bccosA=1+12-4$\sqrt{3}×\frac{\sqrt{3}}{2}$=7,
∴a=$\sqrt{7}$…10分
点评 本题主要考查了正弦定理,余弦定理,正弦函数的图象和性质在解三角形中的综合应用,属于基础题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19.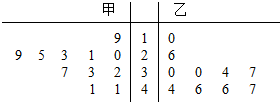 某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )
某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )
 某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )
某苗圃基地为了解基地内甲、乙两块地种植同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用茎叶图表示上述两组树苗高度的数据,对两块地抽取树苗的高度的平均数$\overline{x}$甲,$\overrightarrow{x}$乙和方差进行比较,下面结论正确的是( )| A. | $\overline{x}$甲>$\overrightarrow{x}$乙,乙地树苗高度比甲地树苗高度更稳定 | |
| B. | $\overline{x}$甲<$\overrightarrow{x}$乙,甲地树苗高度比乙地树苗高度更稳定 | |
| C. | $\overline{x}$甲<$\overrightarrow{x}$乙,乙地树苗高度比甲地树苗高度更稳定 | |
| D. | $\overline{x}$甲>$\overrightarrow{x}$乙,甲地树苗高度比乙地树苗高度更稳定 |
20.已知集合A={x||x|≤3},B={x|y=ln(2-x)},则A∪B=( )
| A. | (-∞,3] | B. | (-∞,-3) | C. | [2,3) | D. | [-3,2) |