题目内容
1.已知数列{an}中,a1=1,an+1=an+n.(1)写出数列{an}的前5项;
(2)猜想数列{an}的通项公式.
分析 (1)数列{an}中,由a1=1,an+1=an+n分别令n=1,2,3,4,能够依次求出a2,a3,a4,a5.
(2)由数列的前5项,猜想.再用累加法证明.
解答 解:(1)a1=1,an+1=an+n,
∴a2=a1+1=1+1=2,
a3=a2+2=2+2=4,
a4=a3+3=4+3=7,
a5=a4+4=7+4=11,
(2)猜想an=$\frac{1}{2}$n(n-1)+1,
理由如下:
∵a2-a1=1,
a3-a2=2,
a4-a3=3,
…,
an-an-1=n-1,
累加得到,an-a1=1+2+…+(n-1)=$\frac{1}{2}$n(n-1),
∴an=$\frac{1}{2}$n(n-1)+1,猜想成立.
点评 本题考查数列的递推公式的应用,解题时要仔细观察,合理猜想,注意累加法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知a>-2,若圆O1:x2+y2+2x-2ay-8a-15=0,圆O2:x2+y2+2ax-2ay+a2-4a-4=0恒有公共点,则a的取值范围为( )
| A. | (-2,-1]∪[3,+∞) | B. | $(-\frac{5}{3},-1)∪(3,+∞)$ | C. | $[-\frac{5}{3},-1]∪[3,+∞)$ | D. | (-2,-1)∪(3,+∞) |
12.已知tanα=2,则tan(α-$\frac{π}{6}$)=( )
| A. | 8-5$\sqrt{3}$ | B. | 6-5$\sqrt{3}$ | C. | 5$\sqrt{3}$-8 | D. | 5$\sqrt{3}$-6 |
 设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.
设k≠0,若函数y1=(x-k)2+2k和y2=-(x+k)2-2k的图象与y轴依次交于A,B两点,函数y1,y2的图象的顶点分别为C,D.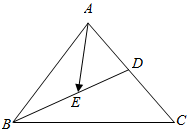 如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.
如图,△ABC中,D为AC中点,E为BD中点,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{b}$.