题目内容
9.已知函数f(x)=[2sin(x+$\frac{2π}{3}$)+sinx]cosx-$\sqrt{3}$sin2x.(1)求函数f(x)的最小正周期;
(2)若实数t∈[0,$\frac{5π}{12}$],求函数f(x)的值域.
分析 (1)先利用降幂公式进行化简,然后利用辅助角公式将f(x)化成$\sqrt{3}$cos2x,最后根据余弦函数的对称性求出对称轴方程即可;
(2)根据t的范围,求出2t的范围,再结合余弦函数单调性求出函数的值域.
解答 解:(1)∵f(x)=[2sin(x+$\frac{2π}{3}$)+sinx]cosx-$\sqrt{3}$sin2x
=[2(sinxcos$\frac{2π}{3}$+cosxsin$\frac{2π}{3}$)+sinx]cosx-$\sqrt{3}$sin2x
=[-sinx+$\sqrt{3}$cosx+sinx]cosx-$\sqrt{3}$sin2x
=$\sqrt{3}$cos2x-$\sqrt{3}$sin2x
=$\sqrt{3}$cos2x,
∴T=$\frac{2π}{2}$=π,
(2)当t∈[0,$\frac{5}{12}$π]时,2t∈[0,$\frac{5}{6}$π],
从而f(t)∈[-$\frac{3}{2}$,$\sqrt{3}$],即f(x)的值域是[-$\frac{3}{2}$,$\sqrt{3}$].
点评 本题主要考查了余弦函数的对称性,以及余弦函数的值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知复数z=1+$\sqrt{3}$i,则$\frac{z^2}{z-2}$=( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
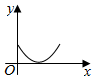
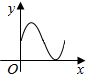
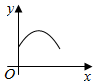
 如图,圆与两坐标轴分别切于A,B两点,圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点,则△OBP的面积随时间变化的图象符合( )
如图,圆与两坐标轴分别切于A,B两点,圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点,则△OBP的面积随时间变化的图象符合( )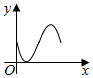
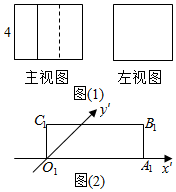 某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )