题目内容
8.抛物线y2=x与直线x-2y-3=0的两个交点分别为P、Q,点M在抛物线上从P向Q运动(点M不同于点P、Q),(Ⅰ)求由抛物线y2=x与直线x-2y-3=0所围成的封闭图形面积;
(Ⅱ)求使△MPQ的面积为最大时M点的坐标.
分析 (Ⅰ)由$\left\{\begin{array}{l}{y^2}=x\\ x-2y-3=0\end{array}\right.$得抛物线与直线的交点为P,Q,根据定积分的即可求出相对应的面积,方法一,选取积分变量为x,方法二,选取积分变量为y
(Ⅱ)设点M的坐标为(a,b),要使△MPQ的面积最大即使点M到直线x-2y-3=0的距离最大,故过点M的切线与直线x-2y-3=0平行,利用导数求出切线的斜率,即可求出a的值,问题得以解决.
解答 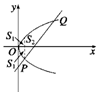 解 (Ⅰ)方法一 由$\left\{\begin{array}{l}{y^2}=x\\ x-2y-3=0\end{array}\right.$得抛物线与直线的交点为P(1,-1),Q(9,3)(如图).
解 (Ⅰ)方法一 由$\left\{\begin{array}{l}{y^2}=x\\ x-2y-3=0\end{array}\right.$得抛物线与直线的交点为P(1,-1),Q(9,3)(如图).
∴S=${∫}_{0}^{1}$[$\sqrt{x}$-(-$\sqrt{x}$)]dx+${∫}_{1}^{9}$($\sqrt{x}$-$\frac{x-3}{2}$)dx=2${∫}_{0}^{1}$$\sqrt{x}$dx+${∫}_{1}^{9}$($\sqrt{x}$-$\frac{x}{2}$+$\frac{3}{2}$)dx
=$\frac{4}{3}$$\sqrt{x^3}$|${\;}_{0}^{1}$+($\frac{2}{3}$x${\;}^{\frac{3}{2}}$-$\frac{x^2}{4}$+$\frac{3}{2}x$|${\;}_{1}^{9}$=$\frac{4}{3}$+$\frac{28}{3}$=$\frac{32}{3}$.
方法二 若选取积分变量为y,则两个函数分别为x=y2,x=2y+3.由方法一知上限为3,下限为-1.
∴S=${∫}_{-1}^{3}$(2y+3-y2)dy=(y2+3y-$\frac{1}{3}$y3)|${\;}_{-1}^{3}$=(9+9-9)-(1-3+$\frac{1}{3}$)=$\frac{32}{3}$.
(Ⅱ)设点M的坐标为(a,b),要使△MPQ的面积最大即使点M到直线x-2y-3=0的距离最大,
故过点M的切线与直线x-2y-3=0平行,
故过点M的切线斜率为k=$\frac{1}{2}$,
∵y2=x,
∴y=$\sqrt{x}$
令y=$\sqrt{x}$,
∴y′=$\frac{1}{2\sqrt{x}}$
∴k=$\frac{1}{2\sqrt{a}}$=$\frac{1}{2}$,
解得a=1,
∴b=1,
∴M点的坐标为(1,1)时,△PAB的面积最大.
点评 本题考查了定积分的有关计算和抛物线的简单性质,以及导数的几何意义,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<b<a |
| A. | (-$\frac{π}{6}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | ($\frac{π}{6}$,$\frac{2π}{3}$) | D. | ($\frac{π}{3}$,$\frac{5π}{6}$) |
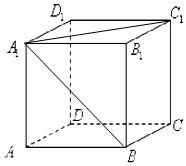 如图,正方体ABCD-A1B1C1D1棱长为1.
如图,正方体ABCD-A1B1C1D1棱长为1.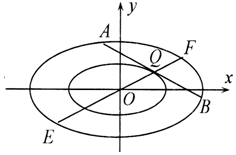 在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.
在直角坐标系xOy中,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,左、右焦点分别是F1,F2,P为椭圆C1上任意一点,|PF1|+|PF2|的最大值为4.