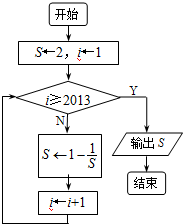
题目内容
已知函数f(x)=
.
(1)写出函数的对称中心;
(2)求函数f(
)的值域.
| 2x-1 |
| x+1 |
(1)写出函数的对称中心;
(2)求函数f(
| x |
考点:函数的图象
专题:函数的性质及应用
分析:(1)根据分式函数的性质,利用分子常数化,即可求出函数的对称中心;
(2)利用换元法结合分式函数的单调性即可求函数f(
)的值域.
(2)利用换元法结合分式函数的单调性即可求函数f(
| x |
解答:
解:(1)f(x)=
=
=2-
,
则函数的对称中心为(-1,2);
(2)设t=
,则t≥0,
则函数f(
)等价为f(t)=2-
,
则函数f(t)=2-
在[0,+∞)上为增函数,
则f(t)≥f(0)=2-3=-1,
即函数f(
)的值域为[-1,+∞)
| 2x-1 |
| x+1 |
| 2(x+1)-3 |
| x+1 |
| 3 |
| x+1 |
则函数的对称中心为(-1,2);
(2)设t=
| x |
则函数f(
| x |
| 3 |
| t+1 |
则函数f(t)=2-
| 3 |
| t+1 |
则f(t)≥f(0)=2-3=-1,
即函数f(
| x |
点评:本题主要考查分式函数的图象和性质,利用分子常数化以及换元法是解决本题的关键.

练习册系列答案
相关题目
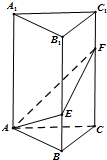 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=