题目内容
13.若$|{\overrightarrow a}|=1,|{\overrightarrow b}|=2$,且$\overrightarrow a,\overrightarrow b$的夹角为60°,则$|{\overrightarrow a+\overrightarrow b}|$的值$\sqrt{7}$.分析 根据向量的数量积公式和向量的模计算即可
解答 解:$|{\overrightarrow a}|=1,|{\overrightarrow b}|=2$,且$\overrightarrow a,\overrightarrow b$的夹角为60°,
则$|{\overrightarrow a+\overrightarrow b}|$2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos60°=1+4+2×1×2×$\frac{1}{2}$=7,
则$|{\overrightarrow a+\overrightarrow b}|$=$\sqrt{7}$,
故答案为:$\sqrt{7}$.
点评 本题考查了向量的数量积公式和向量的模,属于基础题

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
5.某市春节期间7家超市广告费支出xi(万元)和销售额yi(万元)数据如表:
(Ⅰ)若用线性回归模型拟合y与x的关系,求y与x的线性回归方程.
(Ⅱ)若用二次函数回归模型拟合y与x的关系,可得回归方程:$\hat y=-0.17{x^2}$+5x+20,经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出3万元时的销售额.
参考数据:$\overline x=8,\overline y=42,\sum_{i=1}^7{x_i}{y_i}=2794,\sum_{i=1}^7{{x_i}^2}$=708.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$.
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(Ⅱ)若用二次函数回归模型拟合y与x的关系,可得回归方程:$\hat y=-0.17{x^2}$+5x+20,经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出3万元时的销售额.
参考数据:$\overline x=8,\overline y=42,\sum_{i=1}^7{x_i}{y_i}=2794,\sum_{i=1}^7{{x_i}^2}$=708.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{x_i}{y_i}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$$,\hat a=\overline y-\hat b\overline x$.
1.执行如图所示程序框图,则输出的S的值为( )


| A. | 4 | B. | 8 | C. | -20 | D. | -4 |
8.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{BC}=(-4,1)$,向量$\overrightarrow{AC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
18.非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{3}$|$\overrightarrow{b}$|,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$-3$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
5.函数f(x)=(2x-1)ex的递增区间为( )
| A. | (-∞,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $({-\frac{1}{2},+∞})$ |
2.若a是从区间[0,3]中任取的一个实数,则1<a<2的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
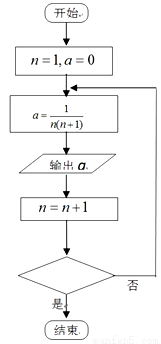
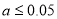 ”,请写出输出的所有数值;
”,请写出输出的所有数值;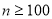 ”,试求出所有输出数字的和。
”,试求出所有输出数字的和。