题目内容
对具有线性相关关系的变量x,y测得一组数据如下表:
根据上表,利用最小二乘法得到它们的回归直线方程为
=10.5x+
.据此模型预测x=30时,y的估计值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 80 | 100 |
 |
| y |
 |
| a |
| A、320 | B、320.5 |
| C、322.5 | D、321.5 |
考点:线性回归方程
专题:概率与统计
分析:求出样本中心坐标,代入回归方程求出
,然后代入模型预测x=30,求出y的估计值.
| ? |
| a |
解答:
解:由题意可知样本中心横坐标
=
=5.
纵坐标为:
=
=60.
回归直线
=10.5x+
.经过样本中心,所以60=10.5×5+
,
∴
=7.5.
回归直线方程为
=10.5x+7.5.
模型预测x=30时,y的估计值:10.5×30+7.5=322.5.
故选:C.
. |
| x |
| 2+4+5+6+8 |
| 5 |
纵坐标为:
. |
| y |
| 20+40+60+80+100 |
| 5 |
回归直线
 |
| y |
 |
| a |
| ? |
| a |
∴
| ? |
| a |
回归直线方程为
 |
| y |
模型预测x=30时,y的估计值:10.5×30+7.5=322.5.
故选:C.
点评:本题考查回归直线方程的应用,基本知识的考查.

练习册系列答案
相关题目
在三角形ABC中,acosB=bcosA,则三角形ABC是( )
| A、钝角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |
已知函数f(x)=2x(-2≤x≤2),则函数y=f(2x)-2f(x)的最大值是( )
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、8 |
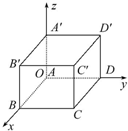 如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,
如图,已知长方体ABCD-A′B′C′D的边长为AB=12,AD=8,AA′=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA′分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,