设点P是椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{25}$=1上的一点.F1.F2是椭圆的两个焦点.若PF1⊥PF2.则|PF1|与|PF2|差的绝对值是( )A．0B．2$\sqrt{5}$C．4$\sqrt{5}$D．2$\sqrt{15}$ 题目和参考答案——青夏教育精英家教网——

题目内容

16．设点P是椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{25}$=1上的一点，F₁，F₂是椭圆的两个焦点，若PF₁⊥PF₂，则|PF₁|与|PF₂|差的绝对值是（　　）

A．

0

B．

2$\sqrt{5}$

C．

4$\sqrt{5}$

D．

2$\sqrt{15}$

分析通过设|PF₁|=t，利用椭圆方程及其定义可知|PF₂|=10-t，进而利用勾股定理解方程即得结论．

解答解：设|PF₁|=t，由椭圆方程及其定义，可知|PF₂|=10-t，
∵PF₁⊥PF₂，
∴△PF₁F₂为直角三角形，
由勾股定理可知：4×（25-5）=t²+（10-t）²，
整理得：t²-10t+10=0，
解得：t=$\frac{10±\sqrt{100-40}}{2}$=5±$\sqrt{15}$，
∴||PF₁|-|PF₂||=5+$\sqrt{15}$-（5-$\sqrt{15}$）=2$\sqrt{15}$，
故选：D．

点评本题考查椭圆的简单性质，涉及椭圆的定义、勾股定理等基础知识，注意解题方法的积累，属于中档题．

练习册系列答案

学习之友系列答案

学生活动手册系列答案

每周最佳方案系列答案

名校1号系列答案

学习辅导报系列答案

全优考评一卷通系列答案

课外作业系列答案

综合复习与测试系列答案

课时总动员系列答案

期末赢家系列答案

相关题目

6．若展开式（x+1）ⁿ中第六项的系数最大，求展开式的第二项．

7．正方体ABCD-A₁B₁C₁D₁的棱长为1，E，F分别为BB₁，CD的中点，则点F到平面A₁D₁E的距离为（　　）

$\frac{{3\sqrt{2}}}{10}$

$\frac{{3\sqrt{5}}}{10}$

$\frac{{\sqrt{2}}}{10}$

$\frac{{\sqrt{5}}}{10}$

4．已知实数a，b，c满足a＞b＞c，则下列结论正确的是（　　）

11．将半径都为1的4个彼此相切的钢球完全装入形状为正三棱台的容器里，该正三棱台的高的最小值为（　　）

$\frac{2+2\sqrt{6}}{3}$

1+$\frac{{2\sqrt{6}}}{3}$

2+$\frac{{2\sqrt{6}}}{3}$

3+$\frac{{2\sqrt{6}}}{3}$

1．已知函数f（x）=lnx-x+1，记函数f（x）的极大值为m，数列{a_n}的前n项和为S_n，且a₁=m+$\frac{1}{2}$，$\frac{1}{{a}_{n+1}}$=$\frac{{a}_{n}{+a}_{n}^{2}}{{2a}_{n}^{2}}$（a_n≠1）．
（1）证明：数列{$\frac{1}{{a}_{n}}$-1}是等比数列，并求数列{a_n}的通项公式；
（2）证明：2e${\;}^{{S}_{n}}$＞2ⁿ+1．

8．已知四边形ABCD是直角梯形，AB⊥BC，下列结论中成立的是（　　）

$\overrightarrow{DA}$•$\overrightarrow{DC}$＜0

$\overrightarrow{AB}$•$\overrightarrow{DC}$＞0

$\overrightarrow{DC}$•$\overrightarrow{CB}$＜0

$\overrightarrow{AC}$•$\overrightarrow{BD}$＞0

5．若关于x的不等式sin（x+1）≤ax+a的解集为[-1，+∞），则a的取值范围为（　　）

[$\frac{1}{2}$，+∞）

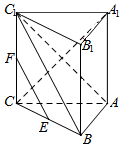如图，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AB⊥AC，AC=AA₁，E、F分别是棱BC、CC₁的中点．
（Ⅰ）若线段AC上的点D满足平面DEF∥平面ABC₁，试确定点D的位置，并说明理由；
（Ⅱ）证明：EF⊥A₁C．