题目内容
数列求和:
+
+
+…+
= .
| 1 |
| 1×(1+2) |
| 1 |
| 2×(2+2) |
| 1 |
| 3×(3+2) |
| 1 |
| n(n+2) |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:
=
(
-
),再叠加,即可得出结论.
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
解答:
解:∵
=
(
-
),
∴
+
+
+…+
=
(1-
+
-
+…+
-
)
=
(1+
-
-
)=
-
.
故答案为:
-
.
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴
| 1 |
| 1×(1+2) |
| 1 |
| 2×(2+2) |
| 1 |
| 3×(3+2) |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 2n+3 |
| (n+1)(n+2) |
故答案为:
| 3 |
| 4 |
| 2n+3 |
| (n+1)(n+2) |
点评:本题考查裂项求和,考查学生的计算能力,确定
=
(
-
)是关键.
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |

练习册系列答案
相关题目
执行如图的程序框,输出k的值是( )


| A、6 | B、5 | C、4 | D、3 |
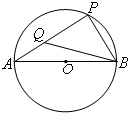 如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且
如图,AB是半径为3的圆O的直径,P是圆O上异于A,B的一点Q是线段AP上靠近A的三等分点,且 甲、乙两位同学某学科的连续五次考试成绩用茎叶图表示如图,则平均分数较高的是
甲、乙两位同学某学科的连续五次考试成绩用茎叶图表示如图,则平均分数较高的是