题目内容
函数f(x)=2x2+x-1,x∈[-5,5],在定义域内任取一点x0,使f(x0)≤0的概率是 .
考点:几何概型
专题:概率与统计
分析:先解不等式f(x0)≤0,得能使事件f(x0)≤0发生的x0的取值长度为3,再由x0总的可能取值,长度为定义域长度10,得事件f(x0)≤0发生的概率是0.3
解答:
解:∵f(x)≤0?2x2+x-1≤0?-1≤x≤0.5,
∴f(x0)≤0?-1≤x0≤0.5,即x0∈[-1,0.5],
∵在定义域内任取一点x0,
∴x0∈[-5,5],
∴使f(x0)≤0的概率P=
=
;
故答案为:
.
∴f(x0)≤0?-1≤x0≤0.5,即x0∈[-1,0.5],
∵在定义域内任取一点x0,
∴x0∈[-5,5],
∴使f(x0)≤0的概率P=
| 1.5 |
| 10 |
| 3 |
| 20 |
故答案为:
| 3 |
| 20 |
点评:本题考查了几何概型的意义和求法,将几何概率转化为长度、面积、体积等之比,是解决问题的关键

练习册系列答案
相关题目
已知两条相交直线a、b,a∥平面α,则b与平面α的位置关系( )
| A、b∥α |
| B、b与α相交 |
| C、b?α |
| D、b∥α或b与α相交 |
函数f(x)=sin(-2x)的一个单调增区间是( )
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
函数f(x)=sinx-cos(x+
)的单调递增区间为( )
| π |
| 6 |
A、[2kπ-
| ||||
B、[2kπ-
| ||||
C、[2kπ-
| ||||
D、[2kπ-
|
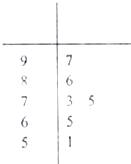 某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100分为A等,70分-84分为B等,55分-69分为C等,54分以下为D等.右边的茎叶图(十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩.