Question

20．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0\;，\;\;b＞0）$的左、右焦点分别为F₁，F₂，且焦点与椭圆$\frac{x^2}{36}+\frac{y^2}{2}=1$的焦点相同，离心率为$e=\frac{{\sqrt{34}}}{5}$，若双曲线的左支上有一点M到右焦点F₂的距离为18，N为MF₂的中点，O为坐标原点，则|NO|等于（　　）

• A． $\frac{2}{3}$
• B． 1
• C． 2
• D． 4

Answer 1

分析 求得椭圆的焦点，可得双曲线的c，由离心率公式可得a，连接MF₁，利用ON是△MF₁F₂的中位线，|ON|=$\frac{1}{2}$|MF₁|，再由双曲线的定义求出|MF₁|，进而得到|ON|的值．

解答 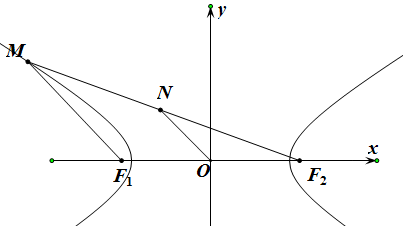解：椭圆$\frac{x^2}{36}+\frac{y^2}{2}=1$的焦点
为（±$\sqrt{34}$，0），
可得双曲线的c=$\sqrt{34}$，
离心率为$e=\frac{{\sqrt{34}}}{5}$，可得a=5，
由双曲线左支上有一点M到右焦点F₂的距离为18，
N是MF₂的中点，
连接MF₁，
ON是△MF₁F₂的中位线，
可得ON∥MF₁，
|ON|=$\frac{1}{2}$|MF₁|，
由双曲线的定义知，|MF₂|-|MF₁|=2×5，
∴|MF₁|=8．
∴|ON|=4，
故选：D．

点评 本题考查椭圆的焦点和双曲线的焦点，考查双曲线的定义，考查三角形中位线的性质，属于中档题．