题目内容
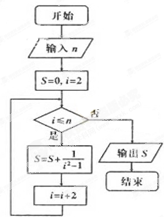
某县共有28个单位，为检查干部的上班情况，将其每个单位编号，编号依次为01到28．现用系统抽样方法抽取4个单位进行检查．若得到的编号的和为54，则抽到的最小编号为（ ）
| A、2 | B、3 | C、4 | D、5 |
考点：系统抽样方法
专题：概率与统计
分析：求出系统抽样的抽取间隔，设抽到的最小编号x，根据编号的和为54，求x即可．
解答：
解：系统抽样的抽取间隔为
=7．
设抽到的最小编号x，
则x+（7+x）+（14+x）+（21+x）=54⇒x=3．
故选：B．
| 28 |
| 4 |
设抽到的最小编号x，
则x+（7+x）+（14+x）+（21+x）=54⇒x=3．
故选：B．
点评：本题考查了系统抽样方法，熟练掌握系统抽样的特征是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
复数z=
（i为虚数单位），则z的共轭复数
为（ ）
| 2 |
| 1-i |
. |
| z |
| A、1-i | B、1+i |
| C、3-i | D、3+i |
某校为了解网瘾学生上网情况，抽查了100名同学，统计他们暑假期间每天平均上网时间，绘成频率分布直方图（如图）．则这100名同学中每天平均上网时间在6～8小时内的同学人数为（ ）| A、30 | B、40 | C、50 | D、60 |
若0＜
＜
的解集记为p，关于x的不等式x2+（a-1）x-a＞0的解集记为q，且p是q的充分不必要条件，则实数a的取值范围是（ ）
| 1 |
| x |
| 1 |
| 2 |
| A、（-2，-1] |
| B、[-2，-1] |
| C、[-1，+∞） |
| D、[-2，+∞） |
从6名教师中选4名开设A，B，C，D四门课程，每人开设一门课程且开设的课程各不相同，若这6名教师中甲、乙两人不开设A课程，则不同的选择方案共有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
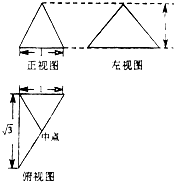
已知三棱锥的三视图如图所示，则它的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x，y满足条件
，则y-（
）x的最大值为（ ）
|
| 1 |
| 2 |
| A、0 | ||
B、
| ||
C、-
| ||
| D、1 |
