题目内容

1．已知${A}_{n+1}^{2}$-${A}_{n}^{2}$=10，则n的值为（　　）
A．4B．5C．6D．7

分析 直接展开排列数公式，化为关于n的一次方程求解．

解答 解：由${A}_{n+1}^{2}$-${A}_{n}^{2}$=10，得
（n+1）n-n（n-1）=10，
即n（n+1-n+1）=10，
∴2n=10，得n=5．
故选：B．

点评 本题考查排列数公式，是基础的计算题．

练习册系列答案
相关题目
11．运用秦九韶算法求n次多项式的值时，考虑到可能有的系数为0，那么最多要进行（　　）次乘法运算．
A．nB．n-1C．n+1D．以上都不对
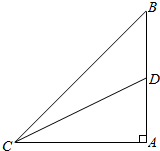12．如图，AB是竖立在地面上的一根杆子，高为10m，D为AB的中点，在地面C处测得点B的仰角为45°，则在C处测点D的仰角应是多少（精确到0.1°）
9．已知f（α）=$\frac{sin（-α+\frac{π}{2}）cos（\frac{3π}{2}-α）tan（α+5π）}{tan（-α-π）sin（α-3π）}$．
（1）化简f（α）；
（2）若α是第三象限角，且cos（$α-\frac{3π}{2}$）=$\frac{1}{5}$，求f（α）的值；
（3）若α=-$\frac{31π}{3}$，求f（a）的值．
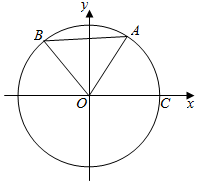16．如图，在平面直角坐标系xOy中，点A，B均在单位圆上，已知点A在第一象限，横坐标为$\frac{\sqrt{3}}{3}$，点B在第二象限．若△AOB为正三角形，则点B的坐标为B（$\frac{\sqrt{3}-3\sqrt{2}}{6}$，$\frac{3+\sqrt{6}}{6}$）．
6．sin2β＞0的充分必要条件是{x|kπ＜β＜kπ+$\frac{π}{2}$，（k∈Z）}．
13．在0°-360°范围内．找出与下列各角终边相同的角，并判定它们是第几象限角．
（1）-120°；
（2）640°；
（3）-950°12′．
3．若函数y=f（x）的导函数y=f′（x）的图象如图所示，则y=f（x）的图象可能（　　）
A．B．C．D．
4．以（-2，1）为圆心且与直线x+y=3相切的圆的方程为（　　）
A．（x-2）2+（y+1）2=2B．（x+2）2+（y-1）2=4C．（x-2）2+（y+1）2=8D．（x+2）2+（y-1）2=8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网