题目内容
2.已知函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$,给出下列结论正确的是( )| A. | f(x)的最小正周期是2π | B. | $f(x)的一条对称轴是x=\frac{π}{6}$ | ||
| C. | $f(x)的一个对称中心是(\frac{π}{6},0)$ | D. | $f(x-\frac{π}{6})是奇函数$ |
分析 利用二倍角的正弦公式化简函数的解析式,再正弦函数的周期性、奇偶性、以及图象的对称性,得出结论.
解答 解:对于函数$f(x)=sin(x+\frac{π}{6})cos(x+\frac{π}{6})$=$\frac{1}{2}$sin(2x+$\frac{π}{3}$),
它的最小正周期为$\frac{2π}{2}$=π,故排除A;
令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈Z,可得它的对称轴方程为x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈Z,故排除B;
令2x+$\frac{π}{3}$=kπ,求得x=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,可得它的对称中心为($\frac{kπ}{2}$-$\frac{π}{6}$,0),k∈Z,故排除C;
根据f(x-$\frac{π}{6}$)=$\frac{1}{2}$sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=$\frac{1}{2}$sin2x,为奇函数,
故选:D.
点评 本题主要考查二倍角的正弦公式,正弦函数的周期性、奇偶性、以及图象的对称性,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.圆Г的圆周上六个点将圆周等分,经过这6个点中任意两点做圆的弦,在所做的这些弦中任意取出两条,则这两条弦有公共点的概率为( )
| A. | $\frac{5}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{15}$ |
13.已知向量$\overrightarrow{a}$=(-1,3),则|$\overrightarrow{a}$|的值是( )
| A. | $\sqrt{10}$ | B. | 10 | C. | $\sqrt{5}$ | D. | 5 |
10.为了研究“数学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
甲班:87、83、90、70、66、71、82、72、67、57、67、72、57、58、68、74、87、78、69、58
乙班:71、80、81、82、90、65、57、73、85、86、91、95、86、67、68、75、96、88、89、69
(Ⅰ)作出甲、乙两班学生成绩茎叶图;并求甲班数学成绩的中位数和乙班学生数学成绩的众数;
(Ⅱ)学校规定:成绩不低于80分的为优秀,请写出下面的2×2联列表,并判断有多大把握认为“成绩游戏与教学方式有关”.
下面临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$)
甲班:87、83、90、70、66、71、82、72、67、57、67、72、57、58、68、74、87、78、69、58
乙班:71、80、81、82、90、65、57、73、85、86、91、95、86、67、68、75、96、88、89、69
(Ⅰ)作出甲、乙两班学生成绩茎叶图;并求甲班数学成绩的中位数和乙班学生数学成绩的众数;
(Ⅱ)学校规定:成绩不低于80分的为优秀,请写出下面的2×2联列表,并判断有多大把握认为“成绩游戏与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
14.已知向量$\overrightarrow{AB}$=(3,1),$\overrightarrow{AC}$=(2,4),则向量$\overrightarrow{BC}$=( )
| A. | (5,5) | B. | (6,4) | C. | (-1,3) | D. | (1,-3) |
11.运用秦九韶算法求n次多项式的值时,考虑到可能有的系数为0,那么最多要进行( )次乘法运算.
| A. | n | B. | n-1 | C. | n+1 | D. | 以上都不对 |
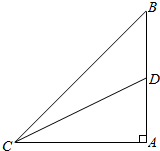 如图,AB是竖立在地面上的一根杆子,高为10m,D为AB的中点,在地面C处测得点B的仰角为45°,则在C处测点D的仰角应是多少(精确到0.1°)
如图,AB是竖立在地面上的一根杆子,高为10m,D为AB的中点,在地面C处测得点B的仰角为45°,则在C处测点D的仰角应是多少(精确到0.1°)