题目内容
4.已知f(x+1)为偶函数,则函数y=f(2x)的图象的对称轴是( )| A. | x=1 | B. | x=$\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=-1 |
分析 根据复合函数的对称性,由f(x+1)是偶函数,故函数f(x+1)的图象关于Y轴对称,此时x=0,括号内x+1=1,故y=f(2x)的图象的对称轴依然要保证括号内的整体2x=1,即x=$\frac{1}{2}$.
解答 解:∵f(x+1)是偶函数,
∴函数f(x+1)的图象关于y轴对称,
∴函数f(x)的图象关于直线x=1对称,
∴函数f(2x)的图象关于直线x=$\frac{1}{2}$对称,
故选B.
点评 求复合函数的对称轴的关键是“以不变应万变”,即不管函数括号里的式子形式怎么变化,括号里式子的取值始终不发生变化.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15.函数f(x)=lnx+2x-6,若实数x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值( )
| A. | 恒为正 | B. | 等于零 | C. | 恒为负 | D. | 不小于零 |
12.下列命题中是假命题的是( )
| A. | 若a>0,则2a>1 | B. | 若x2+y2=0,则x=y=0 | ||
| C. | 若b2=ac,则a,b,c成等比数列 | D. | 若a+c=2b,则a,b,c成等差数列 |
19.全集U={1,2,3,4,5},集合A={1,2},集合B={1,3,5},则图中阴影部分所表示的集合是( )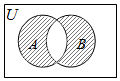

| A. | {1} | B. | {1,2,3,5} | C. | { 2,3,5} | D. | {4} |
13.已知集合M={x|x-2>0,x∈R},N={y|y=$\sqrt{{x}^{2}+1}$,x∈R},则M∩N=( )
| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|x>2} | D. | {x|x>2或x<0} |
14.$\frac{1}{3}$[$\frac{1}{2}$(2a+8b)-(4a-2b)]等于( )
| A. | 2a-b | B. | 2b-a | C. | b-a | D. | -( b-a ) |