题目内容

由数字1，2，3，4组成没有重复数字的自然数共有（　　）
A、(
A
1
4
+
A
2
4
+
A
3
4
+
A
4
4
)个
B、(
A
1
2
+
A
2
2
+
A
3
2
+
A
4
4
)个
C、(
A
1
2
•
A
2
4
•
A
3
4
•
A
4
4
)个
D、
A
4
4
个
考点：排列及排列数公式
专题：排列组合
分析：因为数字1，2，3，4组成没有重复数字的自然数不知是几位数，于是可以分为四类，根据分类计数原理可得．
解答： 解：需要分四类，第一类，是一位数，有
A
1
4
个，
第二类，是两位位数，有
A
2
4
个，
第三类，是三位数，有
A
3
4
个，
第四类，是四位数，有
A
4
4
个，
根据分类计数原理由数字1，2，3，4组成没有重复数字的自然数共有(
A
1
4
+
A
2
4
+
A
3
4
+
A
4
4
)个，
故选：A
点评：本题考查了分类计数问题，关键是如何分类，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2+ln（x+m）与函数g（x）=x2+ex-
1
2
（x＜0）的图象上存在关于y轴对称的点（e为自然对数的底数），则m的取值范围是（　　）
A、（-∞，
e
）
B、（-∞，
1
e
）
C、（-
1
e
，
e
）
D、（-
e
，
1
e
）
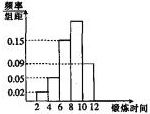某校友200位教职员工，其每周用于锻炼身体所用时间的频率分布直方图如图所示，据图估计，锻炼时间在[8，10]小时内的人数为（　　）
A、76B、82C、88D、95
函数f（x）=
x2-3x+2
的单调增区间是
 
．
已知在等差数列{an}中，对任意正整数n，都有an＞an+1，且a2，a8是方程x2-12x+m=0的两根，且前15项的和为5m，则数列{an}的公差是（　　）
A、-2或-3B、2或3
C、-2D、-3
已知函数f（x）=|ex+
a
ex
|，（a∈R，e是自然对数的底数），在区间[0，1]上单调递增，则a的取值范围是（　　）
A、[0，1]
B、[-1，0]
C、[-1，1]
D、（-∞，-e2）∪[e2，+∞）
试用单调性的定义讨论函数y=x+
1
x
的单调区间，并画出该函数草图．
已知圆x2+y2=2，如果M（x0，y0）是直线x+y+2=0上的一点，那么直线x0x+y0y=2与圆x2+y2=2的位置关系是
 
．
已知an=
1
(2n-1)(2n+1)
，求其前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网