题目内容
7.若等比数列{an}的前项和为Sn,且S2=3,S6=63,则S5=( )| A. | -33 | B. | 15 | C. | 31 | D. | -33或31 |
分析 利用等比数列的通项公式与求和公式即可得出.
解答 解:设等比数列{an}的公比为q≠1,∵S2=3,S6=63,
∴a1(1+q)=3,$\frac{{a}_{1}({q}^{6}-1)}{q-1}$=63,
消去a1,化为q4+q2-20=0,解得q=±2.
q=2时,a1=1;q=-2,a1=-3.
则S5=$\frac{{2}^{5}-1}{2-1}$=31,或S5=$\frac{-3[1-(-2)^{5}]}{1-(-2)}$=-33.
故选:D.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3.如图所示是某几何体的三视图,则该几何体的体积是( )


| A. | 3$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
2.等差数列{an}的前n项和为Sn,且$\frac{S_6}{S_3}=4$,则$\frac{S_9}{S_6}$=( )
| A. | $\frac{9}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{3}$ | D. | 4 |
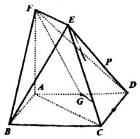 如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.
如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.