如图所示是某几何体的三视图.则该几何体的体积是( )A．3$\sqrt{3}$B．4$\sqrt{3}$C．6$\sqrt{3}$D．9$\sqrt{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

3．如图所示是某几何体的三视图，则该几何体的体积是（　　）

A．

3$\sqrt{3}$

B．

4$\sqrt{3}$

C．

6$\sqrt{3}$

D．

9$\sqrt{3}$

分析由已知中的三视图可得：该几何体是一个以俯视图中大三角形为底面的三棱柱，切去三个以俯视图中小三角形为底面的三棱锥得到的组合体，进而得到答案．

解答解：由已知中的三视图可得：
该几何体是一个以俯视图中大三角形为底面的三棱柱，
切去三个以俯视图中小三角形为底面的三棱锥得到的组合体，
故组合体的体积：V=$\frac{1}{2}$×4×2$\sqrt{3}$×3-3×$\frac{1}{3}$×$\frac{1}{2}$×2×$\sqrt{3}$×3=9$\sqrt{3}$，
故选：D．

点评本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度中档．

练习册系列答案

黄冈课课过关状元成才路系列答案

点拨训练系列答案

北大绿卡系列答案

好卷系列答案

阳光课堂课时优化作业系列答案

左讲右练系列答案

畅优新课堂系列答案

世纪金榜百练百胜系列答案

世纪金榜金榜学案系列答案

黄冈100分闯关系列答案

相关题目

13．已知等比数列{a_n}满足2a₃+a₅=3a₄，且a₃+2是a₂与a₄的等差中项．
（1）求数列{a_n}的通项公式；
（2）设b_n=$\frac{{a}_{n}}{{（a}_{n}-1）{（a}_{n+1}-1）}$，求数列{b_n}的前n项和S_n．

14．在等差数列{a_n}中，a₂+a₈=6，则数列{a_n}的前9项和为27．

11．直线4x-3y=0与圆（x-1）²+（y-3）²=10相交所得弦长为（　　）

18．某手机厂商推出一款6寸大屏手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如表：
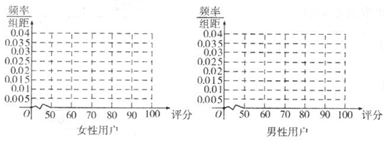
女性用户：

分值区间	[50，60）	[60，70）	[70，80）	[80，90）	[90，100]
频数	20	40	80	50	10

分值区间	[50，60）	[60，70）	[70，80）	[80，90）	[90，100]
频数	45	75	90	60	30

（Ⅰ）完成下列频率分布直方图，并比较女性用户和男性用户评分的波动大小（不要求计算具体值，给出结论即可）；

（Ⅱ）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，再从这20名用户中满足评分不低于80分的用户中任意抽取2名用户，求2名用户评分都小于90分的概率．

8．已知三棱锥S-ABC，满足SA⊥SB，SB⊥SC，SC⊥SA，且SA=SB=SC=3，则该三棱锥外接球的表面积为（　　）

$\frac{27\sqrt{3}π}{2}$

15．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，（$\overrightarrow{a}$-2$\overrightarrow{b}$）•$\overrightarrow{a}$=0，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）

$\frac{2π}{3}$

$\frac{5π}{6}$

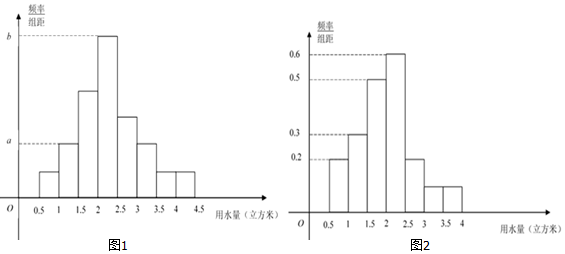
12．某校学生在进行“南水北调工程对北京市民的影响”的项目式学习活动中，对某居民小区进行用水情况随机抽样调查，获得了该小区400位居民某月的用水量数据（单位：立方米），整理得到如下数据分组及频数分布表和频率分布直方图（图1）：

组号	分组	频数
1	[0.5，1）	20
2	[1，1.5）	40
3	[1.5，2）	80
4	[2，2.5）	120
5	[2.5，3）	60
6	[3，3.5）	40
7	[3.5，4）	20
8	[4，4.5）	20

（Ⅰ）求a，b的值；
（Ⅱ）从该小区随机选取一名住户，试估计这名住户一个月用水量小于3立方米的概率；
（Ⅲ）若小区人均月用水量低于某一标准，则称该小区为“节水小区”．假设同组中的每个数据用该组区间的右端点值代替，经过估算，该小区未达到“节水小区”标准，而且该小区居民月用水量不高于这一标准的比例为65%，经过同学们的节水宣传，三个月后，又进行一次同等规模的随机抽样调查，数据如图2所示，估计这时小区是否达到“节水小区”的标准？并说明理由．

7．若等比数列{a_n}的前项和为S_n，且S₂=3，S₆=63，则S₅=（　　）