题目内容
15.已知曲线C的极坐标方程是ρ=2cosθ+4sinθ,P点极坐标为$(3,\frac{π}{2})$,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系xOy,在平面直角坐标系中,直线l经过点P,倾斜角为$\frac{π}{3}$.(1)写出曲线C的直角坐标方程和直线l的参数方程;
(2)设直线l与曲线C相交于A,B两点,求$\frac{1}{|PA|}+\frac{1}{|PB|}$的值.
分析 (1)利用三种方程的转化方程,即可写出曲线C的直角坐标方程和直线l的参数方程;
(2)将参数方程代入曲线C的直角坐标方程,及参数的几何意义,即可得到$\frac{1}{|PA|}+\frac{1}{|PB|}$的值.
解答 解:(1)曲线C的极坐标方程化为直角坐标方程为x2+y2-2x-4y=0,
化为标准方程为:(x-1)2+(y-2)2=5,P$(3,\frac{π}{2})$化为直角坐标为P(0,3),
直线l的参数方程为$\left\{{\begin{array}{l}{x=tcos\frac{π}{3}}\\{y=3+tsin\frac{π}{3}}\end{array}}\right.$即$\left\{{\begin{array}{l}{x=\frac{1}{2}t}\\{y=3+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$(t为参数).…(5分)
(2)将l的参数方程代入曲线C的直角坐标方程,得${(\frac{1}{2}t-1)^2}+{(\frac{{\sqrt{3}}}{2}t+1)^2}=5$,
整理得:${t^2}+(\sqrt{3}-1)t-3=0$,
显然有△>0,则t1+t2=-$\sqrt{3}$+1,t1t2=-3,
|PA|+|PB|=$\sqrt{16-2\sqrt{3}}$,
所以$\frac{1}{|PA|}+\frac{1}{|PB|}$=$\frac{\sqrt{16-2\sqrt{3}}}{3}$.…(10分)
点评 本题考查直线的参数方程和应用,考查韦达定理和运用,考查基本的运算能力,属于中档题.

练习册系列答案
相关题目
11.直线4x-3y=0与圆(x-1)2+(y-3)2=10相交所得弦长为( )
| A. | 6 | B. | 3 | C. | $6\sqrt{2}$ | D. | $3\sqrt{2}$ |
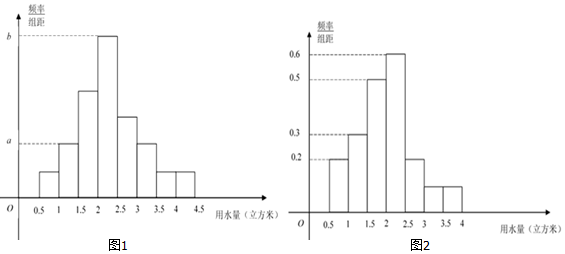
12.某校学生在进行“南水北调工程对北京市民的影响”的项目式学习活动中,对某居民小区进行用水情况随机抽样调查,获得了该小区400位居民某月的用水量数据(单位:立方米),整理得到如下数据分组及频数分布表和频率分布直方图(图1):
(Ⅰ)求a,b的值;
(Ⅱ)从该小区随机选取一名住户,试估计这名住户一个月用水量小于3立方米的概率;
(Ⅲ)若小区人均月用水量低于某一标准,则称该小区为“节水小区”.假设同组中的每个数据用该组区间的右端点值代替,经过估算,该小区未达到“节水小区”标准,而且该小区居民月用水量不高于这一标准的比例为65%,经过同学们的节水宣传,三个月后,又进行一次同等规模的随机抽样调查,数据如图2所示,估计这时小区是否达到“节水小区”的标准?并说明理由.
| 组号 | 分组 | 频数 |
| 1 | [0.5,1) | 20 |
| 2 | [1,1.5) | 40 |
| 3 | [1.5,2) | 80 |
| 4 | [2,2.5) | 120 |
| 5 | [2.5,3) | 60 |
| 6 | [3,3.5) | 40 |
| 7 | [3.5,4) | 20 |
| 8 | [4,4.5) | 20 |
(Ⅱ)从该小区随机选取一名住户,试估计这名住户一个月用水量小于3立方米的概率;
(Ⅲ)若小区人均月用水量低于某一标准,则称该小区为“节水小区”.假设同组中的每个数据用该组区间的右端点值代替,经过估算,该小区未达到“节水小区”标准,而且该小区居民月用水量不高于这一标准的比例为65%,经过同学们的节水宣传,三个月后,又进行一次同等规模的随机抽样调查,数据如图2所示,估计这时小区是否达到“节水小区”的标准?并说明理由.

3.已知Sn是等差数列{an}的前n项和,若a1=-2017,$\frac{{{S_{2014}}}}{2014}-\frac{{{S_{2008}}}}{2008}$=6,则S2017=-2017.
10.已知命题p:负数的立方都是负数,命题q:正数的对数都是负数,则下列命题中是真命题的是( )
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∨(¬q) | D. | (¬p)∧(¬q) |
20.函数$y=\frac{{{x^2}+7x+10}}{x+1}({x>-1})$的最小值为( )
| A. | 2 | B. | 7 | C. | 9 | D. | 10 |
7.若等比数列{an}的前项和为Sn,且S2=3,S6=63,则S5=( )
| A. | -33 | B. | 15 | C. | 31 | D. | -33或31 |