题目内容
函数f(x)=sin(2x-
)的图象为C,给出以下结论:
①图象C关于直线x=
π对称;
②图象C关于点(
,0)对称;
③函数f(x)在区间(-
,
)内是增函数;
④由y=sin2x的图象向右平移
个单位长度可以得到图象C.
其中正确的是( )
| π |
| 3 |
①图象C关于直线x=
| 11 |
| 12 |
②图象C关于点(
| 2π |
| 3 |
③函数f(x)在区间(-
| π |
| 12 |
| 5π |
| 12 |
④由y=sin2x的图象向右平移
| π |
| 3 |
其中正确的是( )
| A、①②④ | B、①②③④ |
| C、①②③ | D、②③④ |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,三角函数的图像与性质
分析:①代入x=
π,判断是否是最值点,即可判断;②代入x=
,判断是否为零点,即可判断;
③令2kπ-
≤2x-
≤2kπ+
(k为整数),求出增区间,通过k的取值,即可判断;
④根据图象左右平移,针对自变量x而言,左加右减,即可判断.
| 11 |
| 12 |
| 2π |
| 3 |
③令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
④根据图象左右平移,针对自变量x而言,左加右减,即可判断.
解答:
解:①x=
π时,f(x)=sin(
-
)=sin
=-1,为最小值,故①对;
②x=
时,f(x)=sin(
-
)=0,故为对称中心,故②对;
③令2kπ-
≤2x-
≤2kπ+
(k为整数),则kπ-
≤x≤kπ+
,k=0即为
区间(-
,
),故③对;
④由y=sin2x的图象向右平移
个单位长度得到函数y=sin2(x-
)的图象,故④错.
故选C.
| 11 |
| 12 |
| 11π |
| 6 |
| π |
| 3 |
| 3π |
| 2 |
②x=
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
③令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
区间(-
| π |
| 12 |
| 5π |
| 12 |
④由y=sin2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
故选C.
点评:本题考查三角函数的图象和性质,主要为对称性和单调性及运用,图象变换的规律,属于易错题.

练习册系列答案
相关题目
若f(x),g(x)分别是R上的奇函数,偶函数,且f(x)-g(x)=ex,则有( )
| A、g(0)<f(2)<f(3) |
| B、f(2)<f(3)<g(0) |
| C、g(0)<f(3)<f(2) |
| D、f(2)<g(0)<f(3) |
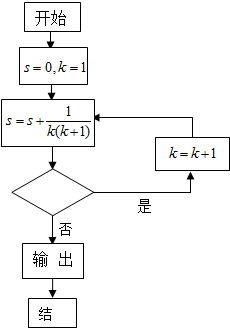
若如图所示的框图所给程序运行的结果S=
,那么判断框中可以填入的关于实数k的判断条件应是( )
| 2010 |
| 2011 |

| A、k<2010 |
| B、k<2009 |
| C、k>2010 |
| D、k>2009 |
设{an}是首项大于零的等比数列,则“a1>a2”是“数列{an}为递减数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知向量
、
满足|
|=1,|
+
|=3,则|
|的取值范围为( )
| a |
| b |
| a |
| a |
| b |
| b |
| A、[1,2] |
| B、[0,4] |
| C、[1,3] |
| D、[2,4] |
 如图,将边长为2的正方形ABCD沿对角线BD折起得到一个三棱锥C-ABD,已知该三棱锥的正视图与俯视图如图所示,则其侧视图的面积为( )
如图,将边长为2的正方形ABCD沿对角线BD折起得到一个三棱锥C-ABD,已知该三棱锥的正视图与俯视图如图所示,则其侧视图的面积为( )