题目内容
周长为6的等腰△ABC中,当顶角A=
时,S△ABC的最大值为
,周长为4的扇形OAB中,则当圆心角α,|α|=∠AOB= (弧度)时,S扇形△AOB的最大值是1.
| π |
| 3 |
| 3 |
考点:弧长公式
专题:计算题,三角函数的求值
分析:设扇形的弧长为:l,半径为r,所以2r+l=4,所以l=4-2r,表示出面积,利用基本不等式,即可得出结论.
解答:
解:设扇形的弧长为:l,半径为r,所以2r+l=4,所以l=4-2r,
S面积=
lr=
×(4-2r)r=(2-r)r≤(
)2=1,
当且仅当r=1,l=2时,S扇形△AOB的最大值是1,此时|α|=∠AOB=2
故答案为:2
S面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2-r+r |
| 2 |
当且仅当r=1,l=2时,S扇形△AOB的最大值是1,此时|α|=∠AOB=2
故答案为:2
点评:本题考查弧度制下,扇形的面积及弧长公式的运用,注意与角度制下的公式的区别与联系.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若菱形ABCD的边长为2,则|
-
+
|等于( )
| AB |
| CB |
| CD |
| A、2 | ||
| B、1 | ||
C、2
| ||
D、
|
化简4x
(-3x
y-
)÷(-6x-
y-
)=( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
A、2xy
| ||
B、-2xy
| ||
| C、2y | ||
| D、-2y-1 |
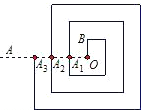 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、