题目内容
7．已知函数f（x）=$\left\{\begin{array}{l}{10x-1，x≤0}\\{{e}^{x}，x＞0}\end{array}\right.$（e为自然对数的底）．若函数g（x）=f（x）-kx恰好有两个零点，则实数k的取值范围是（ ）| A． | （1，e） | B． | （e，10] | C． | （1，10] | D． | （10，+∞） |
分析 令g（x）=0得出f（x）=kx，做出y=kx与y=f（x）的函数图象，则两图象有两个交点，求出y=f（x）的过原点的切线的斜率即可得出k的范围．
解答 解：令g（x）=0得f（x）=kx，
∵g（x）有两个零点，
∴直线y=kx与y=f（x）有两个交点，
做出y=kx和y=f（x）的函数图象，如图所示：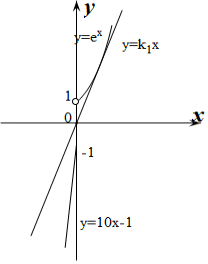
设y=k1x与曲线y=ex相切，切点为（x0，y0），
则$\left\{\begin{array}{l}{{k}_{1}={e}^{{x}_{0}}}\\{{y}_{0}={e}^{{x}_{0}}}\\{{y}_{0}={k}_{1}{x}_{0}}\end{array}\right.$，解得$\left\{\begin{array}{l}{{x}_{0}=1}\\{{y}_{0}=e}\\{{k}_{1}=e}\end{array}\right.$．
∵y=kx与y=f（x）有两个交点，
∴k的取值范围是（e，10]．
故选B．
点评 本题考查了函数零点的个数与函数的图象的关系，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
17．已知函数f（x）=log3|x-t|是偶函数，记$a=f（{{{log}_{0.3}}4}），b=f（{{π^{1.5}}}），c=f（{2-t}）$则a，b，c的大小关系为（ ）
| A． | a＜c＜b | B． | a＜b＜c | C． | c＜a＜b | D． | c＜b＜a |
2．
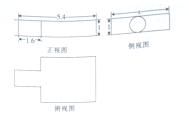中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升，其三视图（单位：寸）如图所示，若π取3，其体积为12.6（立方寸），则图中x的为（ ）| A． | 2.5 | B． | 3 | C． | 3.2 | D． | 4 |
12．
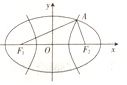如图F1，F2是双曲线${C_1}：{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点，点A是C1，C2在第一象限内的公共点，若|F1F2|=|F1A|，则C2的离心率是（ ）
如图F1，F2是双曲线${C_1}：{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点，点A是C1，C2在第一象限内的公共点，若|F1F2|=|F1A|，则C2的离心率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
16．函数f（x）=sin2x+2$\sqrt{3}$cos2x-$\sqrt{3}$，函数g（x）=mcos（2x-$\frac{π}{6}$）-2m+3（m＞0），若存在x1，x2∈[0，$\frac{π}{4}$]，使得f（x1）=g（x2）成立，则实数m的取值范围是（ ）
| A． | （0，1] | B． | [1，2] | C． | [$\frac{2}{3}$，2] | D． | [$\frac{2}{3}$，$\frac{4}{3}$] |