题目内容
7．集合A={x|-1≤x≤2}，B={x|x＜1}，则A∩∁RB=（ ）| A． | {x|x＜1} | B． | {x|-1≤x＜1} | C． | {x|-1≤x≤1} | D． | {x|1≤x≤2} |
分析 先求出CRB，由此利用交集定义能求出A∩∁RB．
解答 解：∵集合A={x|-1≤x≤2}，B={x|x＜1}，
∴CRB={x|x≥1}，
A∩∁RB={x|1≤x≤2}．
故选：D．
点评 本题考查补集、交集的求法，是基础题，解题时要认真审题，注意补集、交集定义的合理运用．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17．若集合A={x|1≤2x≤16}，B={x|log3（x2-2x）＞1}，则A∩B等于（ ）
| A． | （3，4] | B． | [3，4] | C． | （-∞，0）∪（0，4] | D． | （-∞，-1）∪（0，4] |
18．已知实数x，y满足$\left\{\begin{array}{l}y≤1\\ y≥2x-1\\ x+y≥m\end{array}\right.$如果目标函数z=y-x的最小值为-2，则实数m等于（ ）
| A． | 0 | B． | -2 | C． | -4 | D． | 1 |
15．要得到函数y=sin2x的图象，只要将函数y=sin（2x+$\frac{π}{3}$）的图象（ ）
| A． | 向左平移$\frac{π}{6}$单位即可 | B． | 向右平移$\frac{π}{6}$单位即可 | ||
| C． | 向右平移$\frac{π}{3}$单位即可 | D． | 向左平移$\frac{π}{3}$单位即可 |
2．甲、乙两人射击比赛，两人平的概率是$\frac{1}{2}$，甲获胜的概率是$\frac{1}{3}$，则甲不输的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{5}{6}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
12．已知实数a，b满足2a=3，3b=2，则函数f（x）=ax+x-b的零点个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
19．
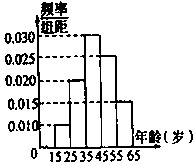某市电视台为了宣传，举办问答活动，随机对该市15至65岁的人群进行抽样，频率分布直方图及回答问题统计结果如表所示：
（1）分别求出a，b，x，y的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取3人颁发幸运奖，求：所抽取的人中第3组至少有1人获得幸运奖的概率．
某市电视台为了宣传，举办问答活动，随机对该市15至65岁的人群进行抽样，频率分布直方图及回答问题统计结果如表所示：| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的概率 |
| 第1组 | [15，25） | 5 | 0.5 |
| 第2组 | [25，35） | a | 0.9 |
| 第3组 | [35，45） | 27 | x |
| 第4组 | [45，55） | b | 0.36 |
| 第5组 | [55，65） | 3 | y |
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组应各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取3人颁发幸运奖，求：所抽取的人中第3组至少有1人获得幸运奖的概率．
17．在正方体ABCD-A1B1C1D1中，CD的中点为M，AA1的中点为N，则异面直线C1M与BN所成角为（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 120° |