题目内容
已知函数f(x)=ex-1-ax,当x∈(0,2]时,讨论函数F(x)=f(x)-xlnx零点个数.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:对F(x)=f(x)-xlnx进行化简,构造函数h(x)=
-xlnx(x>0),研究函数h(x)的单调性和最值,即可确定F(x)=f(x)-xlnx在定义域内是否存在零点;
| ex-1 |
| x |
解答:
解:函数F(x)=f(x)-xlnx的定义域为(0,+∞),
由F(x)=0,得a=
-xlnx(x>0),
令h(x)=
-xlnx(x>0),
则h′(x)=
,
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,2]上单调递增,故h(x)≥h(1)=e-1.
又h(2)=
又当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x,即
>1,
当e-1<a<
<e-1时,函数F(x)有两个不同的零点;
当a=e-1或a=
时,函数F(x)有且仅有一个零点;
当a<e-1或a>
时,函数F(x)没有零点.
由F(x)=0,得a=
| ex-1 |
| x |
令h(x)=
| ex-1 |
| x |
则h′(x)=
| (ex-1)(x-1) |
| x2 |
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,2]上单调递增,故h(x)≥h(1)=e-1.
又h(2)=
| e2-1 |
| 4 |
又当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x,即
| ex-1 |
| x |
当e-1<a<
| e2-1 |
| 4 |
当a=e-1或a=
| e2-1 |
| 4 |
当a<e-1或a>
| e2-1 |
| 4 |
点评:本题以函数为载体,主要考查导数的几何意义,考查导数在研究函数的单调性和最值中的应用,考查恒成立问题的解决方法,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
设i为虚数单位,则复数z=i2+i的实部和虚部分别是( )
| A、-1,i | B、-1,1 |
| C、1,i | D、1,1 |
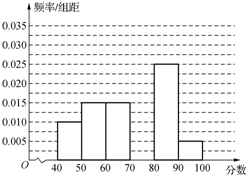 从参加高二年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
从参加高二年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: