Question

已知椭圆

x2

2

+y²=1的左焦点为F，O为坐标原点．
（1）求过点O、F，并且与直线l：x=-2相切的圆的方程；
（2）设过点F且不与坐标轴垂直的直线交椭圆于A、B两点，线段AB的垂直平分线与x轴交于点G，求点G横坐标的取值范围．

Answer 1

考点：直线与圆锥曲线的综合问题,椭圆的简单性质

专题：圆锥曲线中的最值与范围问题

分析：（1）由a²=2，b²=1，可得c=1，F（-1，0），由于圆过点O、F，可得圆心M在直线x=-

1

2

上，设M(-

1

2

，t)，则圆半径 r=|(-

1

2

)-(-2)|=

3

2

，由|OM|=r，得

(- 1 2 )2+t2

=

3

2

，解得t即可得出．
（2）设直线AB的方程为y=k（x+1）（k≠0），代入椭圆方程可得（1+2k²）x²+4k²x+2k²-2=0，由于直线AB过椭圆的左焦点F，可得方程有两个不等实根．设A（x₁，y₁），B（x₂，y₂），AB的中点N（x₀，y₀）．利用中点坐标公式、相互垂直的直线斜率之间的关系可得AB的垂直平分线NG的方程为y-y0=-

1

k

(x-x0)，令y=0，得x_G=-

1

2

+

1

4k2+2

，即可得出．

解答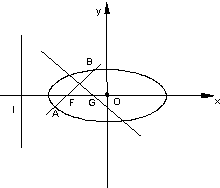： 解：（1）∵a²=2，b²=1，∴c=1，F（-1，0），
∵圆过点O、F，∴圆心M在直线x=-

1

2

上，
设M(-

1

2

，t)，则圆半径 r=|(-

1

2

)-(-2)|=

3

2

，
由|OM|=r，得

(- 1 2 )2+t2

=

3

2

，解得t=±

2

．
∴所求圆的方程为(x+

1

2

)2+(y±

2

)2=

9

4

．
（2）设直线AB的方程为y=k（x+1）（k≠0），
代入

x2

2

+y2=1，整理得（1+2k²）x²+4k²x+2k²-2=0，
∵直线AB过椭圆的左焦点F，∴方程有两个不等实根．
记A（x₁，y₁），B（x₂，y₂），AB的中点N（x₀，y₀）．
∴x₁+x₂=-

4k2

1+2k2

，
∴AB的垂直平分线NG的方程为y-y0=-

1

k

(x-x0)，x0=

x1+x2

2

=

-2k2

1+2k2

，y₀=k（x₀+1）=

k

1+2k2

．
令y=0，得x_G=x₀+ky₀=-

2k2

1+2k2

+

k2

1+2k2

=-

k2

1+2k2

=-

1

2

+

1

4k2+2

，
∵k≠0，∴-

1

2

＜x_G＜0．
∴点G横坐标的取值范围为(-

1

2

，0)．

点评：本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、线段的垂直平分线，考查了推理能力与计算能力，属于难题．