题目内容
已知函数f(x)=ax2-4x-1.
(1)当a=2时,求函数f(x)的零点;
(2)当a=2且x∈(0,1)时,f(1-m)-f(2m-1)<0恒成立,求m的取值范围;
(3)若a=0,设g(x)=
(b≠0),且函数h(x)=g(x)-f(x)是区间(1,3)上的单调函数,求b的取值范围.
(1)当a=2时,求函数f(x)的零点;
(2)当a=2且x∈(0,1)时,f(1-m)-f(2m-1)<0恒成立,求m的取值范围;
(3)若a=0,设g(x)=
| b |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)当a=2时,根据二次函数的零点定义,即可求函数f(x)的零点;
(2)当a=2且x∈(0,1)时,将f(1-m)-f(2m-1)<0恒成立,转化为函数单调性之间的关系,即可求m的取值范围;
(3)根据函数的单调性建立条件关系即可求出b的取值范围.
(2)当a=2且x∈(0,1)时,将f(1-m)-f(2m-1)<0恒成立,转化为函数单调性之间的关系,即可求m的取值范围;
(3)根据函数的单调性建立条件关系即可求出b的取值范围.
解答:
解:(1)当a=2时,f(x)=2x2-4x-1
令f(x)=0,得x1=1+
,x2=1-
,
∴f(x)的零点是1+
和1-
.
(2)∵a=2,∵f(x)=2x2-4x-1=2(x-1)2-3,
∴f(x)在(0,1)上单调递减.
∵当x∈(0,1)时,f(1-m)-f(2m-1)<0恒成立,
可得f(1-m)<f(2m-1),
则
,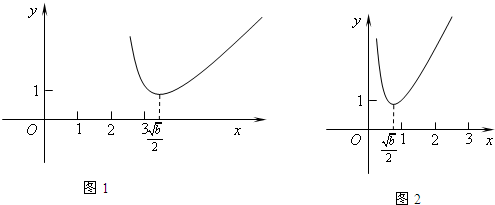
解得
<m<
,
∴m的取值范围是
<m<
.
(3)∵h(x)=
+4x+1(b≠0)
①若b<0,h(x)在(1,3)上为单调增函数,故成立;
②若b>0,则h(x)图象如图:
∵h(x)是(1,3)上的单调函数,
∴
≥3或
≤1,
∴b≥36或0<b≤4.
综上所得,b的取值范围是b<0或0<b≤4或b≥36.
令f(x)=0,得x1=1+
| ||
| 2 |
| ||
| 2 |
∴f(x)的零点是1+
| ||
| 2 |
| ||
| 2 |
(2)∵a=2,∵f(x)=2x2-4x-1=2(x-1)2-3,
∴f(x)在(0,1)上单调递减.
∵当x∈(0,1)时,f(1-m)-f(2m-1)<0恒成立,
可得f(1-m)<f(2m-1),
则
|
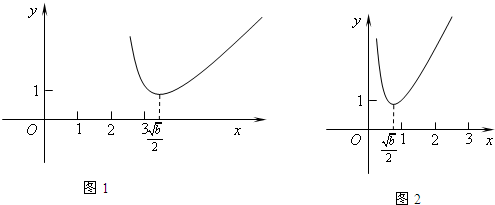
解得
| 1 |
| 2 |
| 2 |
| 3 |
∴m的取值范围是
| 1 |
| 2 |
| 2 |
| 3 |
(3)∵h(x)=
| b |
| x |
①若b<0,h(x)在(1,3)上为单调增函数,故成立;
②若b>0,则h(x)图象如图:
∵h(x)是(1,3)上的单调函数,
∴
| ||
| 2 |
| ||
| 2 |
∴b≥36或0<b≤4.
综上所得,b的取值范围是b<0或0<b≤4或b≥36.
点评:本题主要考查函数单调性的应用,根据函数单调性的性质是解决函数最值的基本方法,考查学生的计算能力,运算量较大,综合性较强.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
圆(x+2)2+y2=5关于坐标原点(0,0)对称的圆的方程是( )
| A、x2+(y-2)2=5 |
| B、x2+(y+2)2=5 |
| C、(x-2)2+y2=5 |
| D、(x-2)2+(y-2)2=5 |
在R上定义运算a?b=a(1-b).若不等式(x+y)?(x-y)<1对于实数x恒成立,则实数y的取值范围是( )
| A、(-2,0) | ||||
| B、(-1,1) | ||||
C、(-
| ||||
D、(-
|