题目内容
不等式|x-a|<b的解为-1<x<2,求2a+b的值.
考点:其他不等式的解法
专题:计算题,不等式的解法及应用
分析:依题意知,b>0,于是解|x-a|<b得a-b<x<a+b,利用不等式|x-a|<b的解为-1<x<2,可求得a与b的值,从而可知2a+b的值.
解答:
解:依题意知,b>0,
由|x-a|<b得:-b<x-a<b,
解得:a-b<x<a+b,
∵原不等式的解为-1<x<2,
∴
,
解得:a=
,b=
,
∴2a+b=
.
由|x-a|<b得:-b<x-a<b,
解得:a-b<x<a+b,
∵原不等式的解为-1<x<2,
∴
|
解得:a=
| 1 |
| 2 |
| 3 |
| 2 |
∴2a+b=
| 5 |
| 2 |
点评:本题考查绝对值不等式的解法,考查等价转化思想与方程思想,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
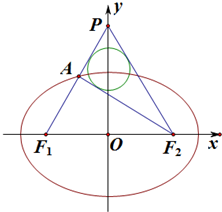 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
对?a、b∈R,运算“⊕”、“?”定义为:a⊕b=
,a?b=
,则下列各式其中不恒成立的是( )
(1)a?b+a⊕b=a+b
(2)a?b-a⊕b=a-b
(3)[a?b]•[a⊕b]=a•b
(4)[a?b]÷[a⊕b]=a÷b.
|
|
(1)a?b+a⊕b=a+b
(2)a?b-a⊕b=a-b
(3)[a?b]•[a⊕b]=a•b
(4)[a?b]÷[a⊕b]=a÷b.
| A、(1)(3) |
| B、(2)(4) |
| C、(1)(2)(3) |
| D、(1)(2)(3)(4) |