题目内容
1.已知数列{an}中,a1=1,前n项和为Sn,对于任意n≥2,3Sn-4,an,2-$\frac{3}{2}$Sn-1总成等差数列.(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{Sn}的前n项和为Tn,求Tn.
分析 (I)对于任意n≥2,3Sn-4,an,2-$\frac{3}{2}$Sn-1总成等差数列.可得2an=3Sn-4+2-$\frac{3}{2}$Sn-1=$\frac{3}{2}$Sn+$\frac{3}{2}$an-2,化为an=3Sn-4,利用递推关系及其等比数列的通项公式即可得出.
(II)利用等比数列的前n项和公式即可得出.
解答 解:(I)对于任意n≥2,3Sn-4,an,2-$\frac{3}{2}$Sn-1总成等差数列.
∴2an=3Sn-4+2-$\frac{3}{2}$Sn-1=$\frac{3}{2}$Sn+$\frac{3}{2}$an-2,化为an=3Sn-4,
∴a1=3a1-4,解得a1=2.
当n≥2时,an-1=3Sn-1-4,可得:an-an-1=3an,
化为${a}_{n}=-\frac{1}{2}$an-1,
∴数列{an}是等比数列,首项为2,公比为-$\frac{1}{2}$.
∴an=$2×(-\frac{1}{2})^{n-1}$.
(II)Tn=$\frac{2[1-(-\frac{1}{2})^{n}]}{1-(-\frac{1}{2})}$=$\frac{4}{3}[1-(-\frac{1}{2})^{n}]$.
点评 本题考查了递推关系、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.当K2>6.635时,认为事件A与事件B( )
| A. | 有95%的把握有关 | B. | 有99%的把握有关 | ||
| C. | 没有理由说它们有关 | D. | 不确定 |
9.把二进制数10102化为十进制数为( )
| A. | 20 | B. | 12 | C. | 11 | D. | 10 |
16.某产品的广告费用支出x与销售额y(单位:百万元)之间有如下的对应数据:
(1)求y与x之间的回归直线方程;(参考数据:22+42+52+62+82=145,2×30+4×40+5×60+6×50+8×70=1380)
(2)试预测广告费用支出为1千万元时,销售额是多少?
附:线性回归方程y=bx+a中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值,线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费用支出为1千万元时,销售额是多少?
附:线性回归方程y=bx+a中,b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值,线性回归方程也可写为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
11.$\root{3}{x\sqrt{x}}$的结果为( )
| A. | x${\;}^{\frac{1}{2}}$ | B. | x${\;}^{\frac{9}{2}}$ | C. | x${\;}^{\frac{3}{2}}$ | D. | x${\;}^{\frac{2}{3}}$ |
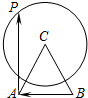 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].