题目内容
4．已知函数f（x）=tanωx在区间（-$\frac{π}{2}$，$\frac{π}{2}$）内是减函数，则ω的取值范围是（ ）| A． | [1，+∞） | B． | （-∞，-1] | C． | [1，0） | D． | （0，1] |
分析 由正切函数的图象与性质，得出关于ω的不等式组，求出解集即可．
解答 解：函数f（x）=tanωx在区间（-$\frac{π}{2}$，$\frac{π}{2}$）内是减函数，
∴ω＜0，且$\frac{π}{|ω|}$≥π，
解得-1≤ω＜0，
∴ω的取值范围是[-1，0）．
故选：C．
点评 本题考查了正切函数的图象与性质的应用问题，是基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
7．在下列条件中，可以判断三角形有两解的是（ ）
| A． | A=30°．B=45°．c=10 | B． | a=$\sqrt{3}$．c=$\sqrt{2}$．B=45° | ||
| C． | a=14．c=16．A=45° | D． | c=7．b=5．C=80° |
8．设全集U={1，2，3，4，5}，集合A={1，2}，B={2，4}，则CU（A∪B）=（ ）
| A． | {1，3，4，5} | B． | {1，4} | C． | {1，2，4} | D． | {3，5} |
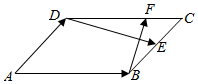如图，在平行四边形ABCD中，E，F分别是BC，DC上的点，且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$，$\overrightarrow{DF}$=2$\overrightarrow{FC}$，记$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，试以$\overrightarrow a，\overrightarrow b$为平面向量的一组基底．利用向量的有关知识解决下列问题；