题目内容
3.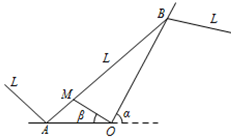 如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=$\frac{3}{{\sqrt{13}}}$,AO=15km.
如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=$\frac{3}{{\sqrt{13}}}$,AO=15km.(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
分析 (1)在△AOM中,利用已知及余弦定理即可解得AM的值;
(2)由cos$β=\frac{3}{\sqrt{13}}$,且β为锐角,可求sinβ,由正弦定理可得sin∠MAO,结合tanα=2,可求sinα,cosα,sin∠ABO,sin∠AOB,结合AO=15,由正弦定理即可解得AB的值.
解答 (本题满分为12分)
解:(1)在△AOM中,A0=15,∠AOM=β,且cosβ=$\frac{3}{\sqrt{13}}$,OM=3$\sqrt{13}$,
由余弦定理可得:AM2=OA2+OM2-2OA•OM•cos∠AOM=(3$\sqrt{13}$)2+152-2×$3\sqrt{13}$×15×$\frac{3}{\sqrt{13}}$=72.
所以可得:AM=6$\sqrt{2}$,大学M在站A的距离AM为6$\sqrt{2}$km.…6分
(2)∵cos$β=\frac{3}{\sqrt{13}}$,且β为锐角,
∴sinβ=$\frac{2}{\sqrt{13}}$,
在△AOM中,由正弦定理可得:$\frac{AM}{sinβ}$=$\frac{OM}{sin∠MAO}$,即$\frac{6\sqrt{2}}{\frac{2}{\sqrt{13}}}$=$\frac{3\sqrt{13}}{sin∠MAO}$,
∴sin∠MAO=$\frac{\sqrt{2}}{2}$,
∴∠MAO=$\frac{π}{4}$,
∴∠ABO=α-$\frac{π}{4}$,
∵tanα=2,
∴sin$α=\frac{2}{\sqrt{5}}$,cosα=$\frac{1}{\sqrt{5}}$,
∴sin∠ABO=sin($α-\frac{π}{4}$)=$\frac{1}{\sqrt{10}}$,
又∵∠AOB=π-α,
∴sin∠AOB=sin(π-α)=$\frac{2}{\sqrt{5}}$.
在△AOB中,AO=15,由正弦定理可得:$\frac{AB}{sin∠AOB}$=$\frac{AO}{sin∠ABO}$,即$\frac{AB}{\frac{2}{\sqrt{5}}}=\frac{15}{\frac{1}{\sqrt{10}}}$,
∴解得AB=30$\sqrt{2}$,即铁路AB段的长AB为30$\sqrt{2}$km.…12分
点评 本题主要考查了正弦定理,余弦定理,同角三角函数关系式,诱导公式的应用,考查了学生运用所学知识解决实际问题的能力,属于中档题.

| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
| A. | $\sqrt{5}$ | B. | $\sqrt{29}$ | C. | $3\sqrt{2}$ | D. | 4 |
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |