题目内容

12．若$（{x^2}+\frac{1}{{\sqrt{x}}}{）^n}$的展开式中存在常数项，则n的一个可能取值是（　　）
A．8B．9C．10D．12

分析 求得展开式的通项公式为Tr+1=${C}_{n}^{r}$•${x}^{2n-\frac{5r}{2}}$，令x的幂指数等于零，求得4n=5r，从而得出结论．

解答 解：根据$（{x^2}+\frac{1}{{\sqrt{x}}}{）^n}$的展开式的通项公式为Tr+1=${C}_{n}^{r}$•${x}^{2n-\frac{5r}{2}}$，令2n-$\frac{5r}{2}$=0，可得4n=5r，
故可取n=10，r=8，
故选：C．

点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．

练习册系列答案
相关题目
2．定义在R上的函数f（x）满足：f（x）=$\frac{{2}^{x}}{f（x-4）}$，则$\frac{f（16）}{f（0）}$=256．
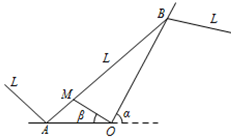3．如图，某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB，位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km，且∠AOM=β，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，且经过大学M，其中tanα=2，cosβ=$\frac{3}{{\sqrt{13}}}$，AO=15km．
（1）求大学M在站A的距离AM；
（2）求铁路AB段的长AB．
20．已知函数f（x）=（ax2+2x-2）ex，其中e是自然对数的底数，a∈R．
（1）若a=1，求曲线f（x）在点（1，f（1））处的切线方程；
（2）若a＜0，求f（x）的单调区间；
（3）若a=-2，函数f（x）的图象与函数$g（x）=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}+m$的图象有3个不同的交点，求实数m的取值范围．
7．由6本不同的书，分成4份，两份各1本，其余两份各2本，则不同的分法有（　　）
A．30B．45C．180D．720
17．等比数列{an}前n和为sn，若s3+s6=s9，则q=±1．
4．设数列{an}的前n项和为Sn，且方程x2-anx-an=0有一根为Sn-1，n=1，2，3，…．
（1）求a1，a2；
（2）计算S1、S2，猜想数列{Sn}的通项公式，并用数学归纳法予以证明．
1．已知函数f（x）=px-$\frac{4p}{x}$-lnx，g（x）=lnx-$\frac{p}{x}$（4+$\frac{{e}^{2}-2e}{{p}^{2}}$），其中无理数e=2.71828…
（1）若p=0，求证：f（x）≥1-x；
（2）若f（x）在其定义域是单调函数，求实数p的取值范围；
（3）对于区间（1，2）中的任意常数p，是否存在x0＞0使f（x0）≤g（x0）成立？若存在，求出符合条件的x0；否则，说明理由．
2．在四棱锥P-ABCD中，四边形ABCD是梯形，AD∥BC，∠ABC=90°，平面PAB⊥平面ABCD，平面 PAD⊥平面ABCD．
（1）求证：PA⊥平面ABCD：
（2）若平面PAB∩平面PCD=l，问：直线l能否与平面ABCD平行？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网