题目内容
8.已知f(x)=-x+sinx,命题p:?x∈(0,$\frac{π}{2}$),f(x)<0,则( )| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
分析 先判断命题P的真假性,再写出该命题的否定命题即可.
解答 解:∵f(x)=-x+sinx,∴f′(x)=-1+cosx≤0
∴f(x)是定义域上的减函数,
∴f(x)≤f(0)=0
∴命题P:?x∈(0,$\frac{π}{2}$),f(x)<0,是真命题;
∴该命题的否定是 ?P:?x0∈(0,$\frac{π}{2}$),f(x0)≥0.
故选:D.
点评 本题考查了命题真假的判断问题,也考查了命题与命题的否定之间的关系,是基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.
如图是教材选修1-2中《推理与证明》一章的知识结构图,请把A处填入适当的方法综合法.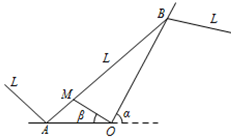 如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=$\frac{3}{{\sqrt{13}}}$,AO=15km.
如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=$\frac{3}{{\sqrt{13}}}$,AO=15km.